- SPIの順列・組み合わせは「中学～高校数学レベル」
- SPIの順列・組み合わせの「例題と解説5選」
➔実際に解いてみる - SPIの順列・組み合わせの解き方のコツや対策方法は「①：公式を覚える②：様々な種類の例題を解く③：解くスピードを上げる」
- SPIの順列・組み合わせに使う公式は、「①：順列②：円順列③：組み合わせ」
- SPIの非言語分野が苦手な人におすすめの対策法は、SPIのアプリを活用すること
-
Webテスト（SPI,玉手箱など）の対策には、以下のツールがおすすめ
-
【就活生/転職者】SPI頻出問題集（LINEで無料配布）
（SPI/Webテストの頻出問題を練習） -
【就活生】Lognavi WEBテスト
（言語・非言語118問,性格診断90問） -
【就活生】適性診断AnalyzeU+
（251問で性格診断）
-
【就活生/転職者】SPI頻出問題集（LINEで無料配布）
この記事では、SPIの「順列・組み合わせ」の練習問題や解き方のコツについて解説します。 あわせて、SPIの順列・組み合わせに使う公式や対策方法を紹介しているのでぜひ参考にしてみてください。
ちなみに、「SPIやテストセンターで落ちたくない」「Webテストを効率的に勉強したい」という人は、SPIやWebテストの例題を短時間で練習できる「SPI頻出問題集（公式LINEで無料配布）」などのサービスを活用しましょう。 この記事を読めば、SPIの順列/組み合わせ(場合の数)の対策をすることができます。 SPIの順列・組み合わせ(場合の数)が苦手な就活生や、SPIの順列・組み合わせ(場合の数)の例題と解説が欲しい就活生はぜひ最後まで読んでください。
「SPIなどのWebテストで落とされたくない！」という方には「SPI頻出問題集」で本番の問題に近い練習をして、効率良く得点をUPさせるのがおすすめです。
ちなみに「SPI頻出問題集」以外にも、SPI模擬テストが受けられる「Lognavi WEBテスト」、251問の性格診断「適性診断AnalyzeU+」もおすすめですよ。
就活アドバイザー 京香
- 【就活生/転職者】SPI頻出問題集（公式LINEで無料配布）
【公式サイト】https://reashu.com/linelp-spi/
- Webテストで頻出の問題がわかる
- 【就活生】Lognavi WEBテスト（言語・非言語118問,性格90問）
【公式サイト】https://lognavi.com/
- 自分の実力を客観的に知れる
- 【就活生】適性診断AnalyzeU+（全251問、客観的な性格診断）
【公式サイト】https://offerbox.jp/
- 診断でSPI性格検査の練習も
「結局どのサービスを使えば良いかわからない…」という方は「SPI頻出問題集」で練習問題を解いてみるのが一番おすすめですよ。
就活アドバイザー 京香
目次
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
【難しい？】SPIの順列・組み合わせ(場合の数)問題の特徴
就活生くん
そもそもSPIを受験したことがないので、順列・組み合わせ(場合の数)の問題がどんなものか分かりません。
就活生ちゃん
私は順列と組み合わせの違いがよく分からないので、教えてほしいです。
ではまず最初にSPIの順列・組み合わせ(場合の数)の特徴をざっくり解説しますね。
「就活の教科書」編集部 しほ
難易度は中学～高校数学レベル
SPIの順列・組み合わせ(場合の数)の問題の難易度は中学～高校数学レベルです。
大学受験で数学を使った人は解き方を覚えていると思います。
ですが、文系の就活生は「解き方を忘れてしまった」という人も多いでしょう。
そのため、SPIの順列・組み合わせ(場合の数)の問題の対策をするには、解き方を思い出す必要があります。
就活生の皆さんは、PとかCとかを使った公式、覚えていますか？
「就活の教科書」編集部 しほ
SPI順列・組み合わせの出題頻度は高い
SPIの順列・組み合わせ(場合の数)の問題は頻出分野です。
web方式、テストセンターともに必ず出題され、問題数も多いです。
難易度がやや高いうえに、頻出分野なので、優先的に対策しておきたい分野です。
順列・組み合わせは必ずSPIで出題されます。
高得点をとるために、必ず対策しましょう。
「就活の教科書」編集部 しほ
SPI順列・組み合わせは対策すれば難しくない
SPIの順列・組み合わせ(場合の数)の問題は、対策すれば誰でも解くことができるようになります。
理由は、順列・組み合わせは、中学生～高校生の数学で学んだ分野だからです。
SPIは解くスピード重視の試験なので、大学受験の数学のように難しい問題は出題されません。
なので、順列・組み合わせの問題も、簡単な対策をすることで、誰でも解けるようになります。
順列・組み合わせができるようになれば、SPIで高得点を取れるようになります。
この記事で対策をして、高得点を目指しましょう。
「就活の教科書」編集部 しほ
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
【解き方も解説】SPI順列・組み合わせ(場合の数)の例題5選
就活生ちゃん
SPI順列・組み合わせ(場合の数)が苦手なので、練習をしたいです。
それでは、SPI順列・組み合わせ(場合の数)の例題と解説を5つ紹介します。
「就活の教科書」編集部 しほ
- 例題①：順列
- 例題②：円順列
- 例題③：組み合わせ-1
- 例題④：組み合わせ-2
- 例題⑤：順列と組み合わせの区別
まず公式を知りたい人は、この記事の「SPI順列・組み合わせ(場合の数)で使う公式一覧」を先に読んでくださいね。
「就活の教科書」編集部 しほ
例題①：順列
ある企業の新卒採用の面接の1日目と2日目の面接官を、A、B、C、Dの4名のうちから1名ずつ選ぶ。
1日目と2日目が同じ人にならないように選ぶとすると、選び方は何通りあるか。
【答え】
12通り
【解説】
1日目の面接官から考えると、1日目の面接官はA、B、C、Dの4名すべてなり得る。
つまり、4通り。
2日目は、1日目に選ばれた人以外の3人から1人選ぶことになる。
つまり、3通り。
したがって、
4×3=12（通り）。
ある会社のプロジェクトチームは、リーダー、サブリーダー、メンバーの3つの役割をA、B、C、Dの4名から選ぶ。ただし、同じ人が複数の役割を兼任しないように選ぶとする。
役割の選び方は何通りあるか？
【答え】
24通り
【解説】
リーダーを選ぶ方法から考える。
リーダーはA、B、C、Dの4名のうち誰でもよいので、4通りの選び方がある。
次に、サブリーダーを選ぶ。
リーダーに選ばれた人以外の3名から選ぶので、3通りの選び方がある。
最後に、メンバーを選ぶ。
リーダーとサブリーダーに選ばれた人以外の2名から選ぶので、2通りの選び方がある。
したがって、リーダー、サブリーダー、メンバーの役割を選ぶ総数は、 4×3×2=24 通りになる。
例題②：円順列
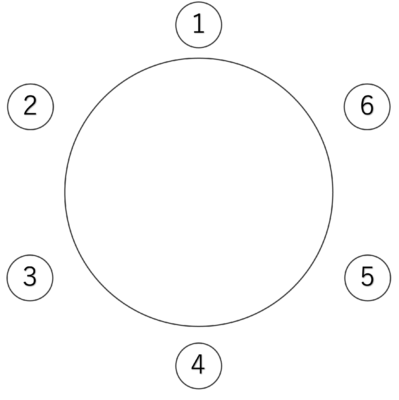
P、Q、R、S、T、Uの6人で、円形のテーブルに座る。
PとQが隣同士になるように6人が座る座り方は何通りか。
【解答】
288通り
【解説】
隣り合う2席は、①②、②③、③④、④⑤、⑤⑥、⑥①の6通り。
また、PQの座り方はそれぞれに（P・Q）、（Q・P）の2通りがある。
よって、6×2=12通り。
残りの4席の決め方は、4！=4×3×2×1=24通り。
これらを掛け合わせて、12×24=288通り。
問題文に「隣り合わせになるように」とある場合は、それらを1つの塊だと考えてから、さらにその中での場合分けを考えます。
「SPIやWebテストの問題をもっと練習したい！」という方は、SPI頻出問題集を使うのがおすすめです。
SPI頻出問題集は、非言語・言語のよく出る問題を網羅しており、効率よく最短でSPIやWebテストの得点アップが狙えますよ。
就活アドバイザー 京香
例題③：組み合わせ-1
X組とY組の生徒が5人ずつ、合わせて10人いる。
この中から掃除当番を4人選びたい。
X組の生徒が3人、Y組の生徒が1人となるように選ぶとすると、掃除当番の選び方は何通りあるか。
【解答】
50通り
【解説】
X組の生徒の選び方は、
5C3=（5×4×3）/（3×2×1）=10通り
Y組の生徒の選び方は、5通り
したがって、
10×5=50通り
例題④：組み合わせ-2
X組とY組の生徒が5人ずつ、合わせて10人いる。
この中から掃除当番を4人選びたい。
X組の生徒が少なくとも1人含まれるように選ぶとすると、掃除登板の選び方は何通りあるか。
【解答】
205通り
【解説】
問題文に「少なくとも」とある時は、「問題文と反対の場合の数」を「全体の場合の数」から引きます。
X組の生徒が1人も含まれない選び方を考えると、
X組0人、Y組4人の場合のみ。
この時の選び方は、Y組の5人から4人を選ぶということなので、
5C4=（5×4×3×1）/（4×3×2×1）=5通り
全体の場合の数は、10人から4人選ぶ組み合わせなので、
10C4=（10×9×8×7）/（4×3×2×1）=210通り
したがって、
210-5=205通り
例題⑤：同じものを含む順列
りんご3個、みかん3個、かき2個がある。
ただし、りんご、みかん、かきの中で区別はないものとする。
ここから4個を取り出したい。
選び方は何通りあるか。
【解答】
10通り
【解説】
同じものを含むので、場合分けして解く。
・3個が同じ場合
- （りんご・りんご・りんご、みかん）
- （りんご・りんご・りんご、かき）
- （みかん・みかん・みかん、りんご）
- （みかん・みかん・みかん、かき）
の4通り
・2個が同じ場合
- （りんご・りんご、みかん・みかん）
- （りんご・りんご、かき・かき）
- （みかん・みかん、かき・かき）
- （りんご・りんご、みかん、かき）
- （みかん・みかん、りんご、かき）
- （かき・かき、りんご、みかん）
の6通り
したがって、
4+6=10通り
SPIの順列・組み合わせ(場合の数)は、どんな問題か分かりましたか？
このように様々な種類の問題があるので、たくさん解いて慣れていきましょう。
「就活の教科書」編集部 しほ
今回参考にした問題集
今回の問題は、こちらの問題集を参考に作成しました。
もっとたくさんの問題を練習したい人は、是非利用してみると対策ができますよ。
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
【短期間でできる】SPIやその他のWebテスト選考を通過するための対策法
就活生くん
SPIや玉手箱、その他のWebテストをいろんな企業の選考で受けないといけないのですが、SPI対策以外にもESや面接などに時間を使いたいです。
短期間で合格ラインまで持っていけるような対策法はないのでしょうか？
短期間でSPIやWebテストの対策をして選考にサクッと通過できるようにしたい就活生は多いです。
そこでここでは、短期間でできるSPIやその他のWebテスト選考を通過するための対策法を紹介しますね。
先に結論を伝えておくと、SPIやWebテストの良く出る問題を練習しておくのが一番おすすめですね！
就活アドバイザー 京香
- 対策法①：SPIやWebテストのよく出る問題を練習しておく
- 対策法②：性格テストの模擬練習をしておく
- 対策法③：SPI対策本を買って苦手分野の問題に取り組む
それでは、それぞれ解説していきます。
就活アドバイザー 京香
対策法①：SPIやWebテストのよく出る問題を練習しておく
短期間でできるSPIやその他のWebテスト選考を通過するための対策法その1は「SPIやWebテストのよく出る問題を練習しておく」ことです。
SPIや玉手箱、Webテストでは、毎回似たような問題が数多く出題されるため、頻出問題だけでも勉強しておくことで合格ラインを越えられることが多いです。
そこで問題をたくさん練習したい方は、SPIやWebテストの問題を網羅した「SPI頻出問題集」を使うのがおすすめです。
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
\ 140,000人以上が利用中！ /
SPIの練習問題を解く
（SPI頻出問題集）
＊公式LINE限定で無料配布中！
SPI頻出問題集は「実際の問題と類似してる点が多く、非常に役立ちました。」という非常に信頼性の高い口コミがありますよ。
就活アドバイザー 京香
対策法②：性格テストの模擬練習をしておく
短期間でできるSPIやその他のWebテスト選考を通過するための対策法その2は「性格テストの模擬練習をしておく」ことです。
実は就活生にはあまり知られていないですが、SPIやWebテストでは性格検査で落ちることがよくあります。
言語や非言語の問題だけを対策していると、性格テストで落ちることになってしまうため、性格テストの対策もする必要があります。
そこでおすすめなのが、本番同様にSPIの性格テストを体験できる「適性診断AnalyzeU+」です。
- 251問の質問があるのでSPIやWebテストの性格検査の対策に向いている
- 100万人のデータから診断してくれるのでかなり正確な結果がわかる
- ついでに診断結果からあなたにおすすめの職種もわかる
\ 大手,優良企業からスカウトが届く! /
客観的な性格診断を受ける
（適性診断AnalyzeU+）
＊プロフィール登録で優良企業のスカウトGET！
適性診断AnalyzeU+は「SPIの性格検査以外にもちゃんと自分の強みがわかる」という点で非常に就活生からの評価が高い診断ですよ。
就活アドバイザー 京香
対策法③：SPI対策本を買って苦手分野の問題に取り組む
短期間でできるSPIやその他のWebテスト選考を通過するための対策法その3は「SPI対策本を買って苦手分野の問題に取り組む」ことです。
SPIの対策本には、どのように対策すべきかやどんな問題が出題されるのかが詳しくまとめられています。
そのため、しっかりと対策したい方にはSPIの参考書をおすすめします。
SPIの問題集を反復して解くうちに、SPIの問題形式になれることが出来ます。
解く時にはしっかりと時間を計測して練習しましょうね。
就活アドバイザー 京香
SPI/テストセンターの対策に役立つ記事一覧
「SPI対策方法が分からない」「SPI対策をしたい」という就活生には以下の記事がおすすめです。
以下の記事を読めば、SPIの能力検査と性格検査対策方法について知れ、選考通過率がアップします。
就活アドバイザー 京香
この記事を読めば、URLを見ただけでWebテストの種類を見分けることができるようになり、どんなWebテストにも対応できるようになります。
就活アドバイザー 京香
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
SPI順列・組み合わせ(場合の数)の解き方のコツや対策方法
就活生ちゃん
SPI順列・組み合わせ(場合の数)が苦手なので、解き方のコツを教えてほしいです。
それでは、SPI順列・組み合わせ(場合の数)を解くときのコツを3つ紹介します。
「就活の教科書」編集部 しほ
- コツ①：公式を覚える
- コツ②：様々な種類の例題を解く
- コツ③：解くスピードを上げる
コツ①：公式を覚える
SPI順列・組み合わせ(場合の数)を解くときのコツ1つ目は、「公式を覚える」です。
「順列・組み合わせ」には最低限覚える必要のある公式が3つあります。
公式を覚えないと、絶対に順列・組み合わせの問題は時間内に解くことができません。
暗記が苦手な人でも、繰り返し問題を解けば、公式は覚えられるので、たくさんの問題を解いて、公式を覚えましょう。
SPI順列・組み合わせ(場合の数)で使う公式は、この記事の「SPI順列・組み合わせ(場合の数)で使う公式一覧」で解説しています。
「就活の教科書」編集部 しほ
コツ②：様々な種類の例題を解く
SPI順列・組み合わせ(場合の数)を解くときのコツ2つ目は、「様々な種類の例題を解く」です。
順列・組み合わせの公式は3つあるため、「どの問題でどの公式を使うのか」を見極める必要があります。
そこで、使う公式を間違えないために、様々な種類の例題を解いて、問題の読解力を上げましょう。
順列・組み合わせの区別は難しいですよね。
問題集を使って、たくさん問題を解くことで、区別できるようになりますよ！
「就活の教科書」編集部 しほ
コツ③：解くスピードを上げる
SPI順列・組み合わせ(場合の数)を解くときのコツ3つ目は、「解くスピードを上げる」です。
SPI非言語は制限時間20分で合計20問に回答する必要があります。
非言語問題の中で、順列・組み合わせは比較的短い時間で回答できます。
ですので、他の難問（推論など）に時間を割くために、順列・組み合わせは解くスピードを上げましょう。
「SPIは時間が足りない！」と悩んでいる就活生は、以下の記事を読めば、SPIの時間配分を対策できます。
「就活の教科書」編集部 しほ
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
SPI順列・組み合わせ(場合の数)で使う公式一覧
就活生ちゃん
SPI順列・組み合わせ(場合の数)で覚えなくてはいけない公式を教えてください！
わかりました！
SPI順列・組み合わせ(場合の数)で使う公式は全部で3つあります。
「就活の教科書」編集部 しほ
公式①：順列
まず1つ目は、順列の公式です。
①n個のものを全部並べる場合、
n ! = n ( n – 1 ) ( n – 2 )・・・× 1
通りある。
②n個のものからr個を取り出して並べる場合、
nPr = n ( n – 1 ) ( n – 2 )・・・{ n – r + 1) }
= n ! / ( n – r ) !
通りある。
実際に練習をしてみましょう。
①A、B、C、D、Eの合計5名の並び方は全部で何通り？
5 ! = 5 × 4 × 3 × 2 × 1 = 120通り
②合計10名のクラスの中から3人を選んで並べる時、全部で何通りできる？
10P3 = 10 × 9 × 8 = 720 通り
公式②：円順列
2つ目は、円順列の公式です。
n個のものを円に並べる場合、
( n – 1 ) !
通りある。
実際に練習をしてみましょう。
A、B、C、D、Eの合計5名が円卓に並んで座るとき、全部で何通りの座り方がある？
( 5 – 1 ) ! = 4 × 3 × 2 × 1 = 24通り
公式③：組み合わせ
3つ目は、組み合わせの公式です。
n個のものからr個を選ぶ組み合わせの数は、
nCr = nPr / r !
通りある。
実際に練習をしてみましょう。
合計10名のクラスの中から3人を委員に選ぶとき、全部で何通りの選び方がある？
10C3 = ( 10 × 9 × 8 ) / ( 3 × 2 ) = 120通り
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
SPI順列・組み合わせ(場合の数)に関するよくある質問
就活生ちゃん
SPI順列・組み合わせ(場合の数)に関して、そのほか知っておくべきことはありますか？
それではSPI順列・組み合わせ(場合の数)に関してよくある質問2つに答えていきますね。
「就活の教科書」編集部 しほ
- 質問①：順列と組み合わせの違いが分からない
- 質問②：SPI順列・組み合わせ(場合の数)は難しいから捨ててもいい？
質問①：順列と組み合わせの違いが分からない
順列と組み合わせの違いは「順番を考慮するかしないか」です。
簡単に見分けるためには、問題文を見ましょう。
問題分に「並べる」や「列」などの言葉が出てきたら順列の公式、「選ぶ」や「組み合わせ」というような言葉が出てきたら組み合わせの公式を使います。
問題文だけでは見分けられないこともあります。
順列と組み合わせは、問題を繰り返し解いて練習することで、見分けられるようになるのがベストです。
「就活の教科書」編集部 しほ
質問②：SPI順列・組み合わせ(場合の数)は難しいから捨ててもいい？
SPI順列・組み合わせ(場合の数)の問題は捨ててはいけません。
理由は、順列・組み合わせはSPIで最頻出分野だからです。
順列・組み合わせを苦手とする就活生は多いですが、練習すれば必ず解けるようになります。
なので、SPIを突破するためには、順列・組み合わせの対策をしましょう。
私も順列・組み合わせは苦手でしたが、何度も解くうちに、分かるようになりました！
「就活の教科書」編集部 しほ
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
SPIの非言語分野が苦手な人におすすめの対策法
就活生ちゃん
数学ができないので、順列・組み合わせ以外も苦手です。
数学ができない人は、どう対策すればいいですか？
就活生は文系の人の方が多いので、数学が苦手な人はたくさんいます。
それでもみなさん対策をして、SPIで高得点を取っています。
そこで、SPIの非言語分野が苦手な人におすすめの対策法を2つ紹介します。
「就活の教科書」編集部 しほ
- SPIの問題集を解く
- SPIのアプリを使う
SPIの問題集を解く
SPI非言語分野が苦手な人におすすめの対策法1つ目は、「SPIの問題集を解く」です。
SPIは反復して問題を解くことで、解き方に慣れることができます。
SPIは「問題傾向を把握すること」が高得点のカギです。
とにかく反復して問題集を解きましょう！
「就活の教科書」編集部 しほ
SPIのアプリを使う
SPI非言語分野問題が苦手な人におすすめの対策法2つ目は、「SPIのアプリを使う」です。
SPI言語・非言語 一問一答は、SPI対策を効率よくすることが出来るスマホアプリです。
SPI言語・非言語 一問一答は、総問題数は300問以上あるからしっかり練習できます。
間違えた問題を自動でチェックしてくれるので、復習にも便利です。
私も、電車移動しているときにアプリでSPIの勉強をしています。
スキマ時間を活用しましょう！
「就活の教科書」編集部 しほ
また、SPI非言語には場合の数以外にも様々な問題があります。
SPI非言語の他の問題については以下の記事で詳しく解説しているので、ぜひ読んでみてください。
「就活の教科書」編集部 しほ
また、中にはSPIの非言語の問題が本当に苦手・・・という就活生もいるのではないでしょうか？
以下の記事ではSPIの非言語が壊滅的でもSPIに通過するのかについて解説しているので、ぜひ読んでみてください。
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
まとめ：数学が苦手な人はSPI順列・組み合わせ(場合の数)の対策が必須
この記事では、「SPIの順列・組み合わせ(場合の数)の問題」について解説しました。
併せて、「SPIの順列・組み合わせ(場合の数)の例題・解説」や、「SPIの順列・組み合わせ(場合の数)の対策法」を紹介しました。
SPIの順列・組み合わせは頻出なので、必ず対策が必要です。
数学が苦手な人は、記事で紹介したSPIの問題集やアプリを使って、順列・組み合わせ(場合の数)の練習をしましょう。
以下がこの記事のまとめです。
◆【特徴を解説】SPIの順列・組み合わせ(場合の数)の問題とは
- 難易度は中学～高校数学レベル
- SPI順列・組み合わせの出題頻度
- SPI順列・組み合わせは対策すれば難しくない
◆【解き方も解説】SPI順列・組み合わせ(場合の数)の例題5選
- 例題①：順列
- 例題②：円順列
- 例題③：組み合わせ-1
- 例題④：組み合わせ-2
- 例題⑤：順列と組み合わせの区別
◆SPI順列・組み合わせ(場合の数)の解き方のコツや対策方法
- コツ①：公式を覚える
- コツ②：様々な種類の例題を解く
- コツ③：解くスピードを上げる
◆SPI順列・組み合わせ(場合の数)で使う公式一覧
- 公式①：順列
- 公式②：円順列
- 公式③：組み合わせ
◆SPI順列・組み合わせ(場合の数)に関するよくある質問
- 質問①：順列と組み合わせの違いが分からない
- 質問②：SPI順列・組み合わせ(場合の数)は難しいから捨ててもいい？
◆SPIの非言語分野が苦手な人におすすめの対策法
- SPIの問題集を解く
- SPIのアプリを使う
◆まとめ：数学が苦手な人はSPI順列・組み合わせ(場合の数)の対策が必須