- SPIの図形問題は「小学校～中学校数学レベル」
- SPIの図形問題はあまり出題されない
- SPIの図形問題の「例題と解説5選」
➔例題を解いてみる - SPIの図形問題は捨てる選択肢もアリ
-
「Webテストで落ちたくない...」なら、以下のツールがおすすめ
-
【就活生/転職者】SPI頻出問題集（LINEで無料配布）
（SPI/Webテストの頻出問題を練習） -
【就活生】Lognavi WEBテスト
（言語・非言語118問,性格診断90問） -
【就活生】適性診断AnalyzeU+
（251問で性格診断）
-
【就活生/転職者】SPI頻出問題集（LINEで無料配布）
-
【就活生/転職者】選考通過ES（LINEで無料配布）
（無料で100枚以上の選考通過したESが見放題） -
【就活生/転職者】LINE適職診断（公式LINEで無料診断）
（あなたの適職を16タイプで診断） -
【就活生/転職者】面接回答集100選（無料公式LINE）
（よく出る質問と模範回答で面接対策）
あわせて、「SPIの図形問題の例題」や「図形問題で覚えておくべき公式」についても紹介しているのでぜひ参考にしてみてください。
ちなみに、「SPIやテストセンターで落ちたくない」「Webテストを効率的に勉強したい」という人は、SPIやWebテストの例題を短時間で練習できる「SPI頻出問題集（公式LINEで無料配布）」などのサービスを活用しましょう。
この記事を読むことで、SPIの図形問題について理解が深まります。「SPIの図形問題で高得点を狙いたいけど対策の仕方が分からない」と悩みを抱えている人はぜひ最後まで読んでください。
SPIの対策ができるおすすめ無料ツール3選
| ①：SPI頻出問題集 |
|---|
 公式LINEで無料配布 |
| ②：Lognavi WEBテスト |
|---|
|
|
| ③：適性検査AnalyzeU+ |
|---|
 全251問、客観的な性格診断
|
「結局どのサービスを使えば良いかわからない…」という方は「SPI頻出問題集」で練習問題を解いてみるのが一番おすすめですよ。
就活アドバイザー 京香
目次
「就活の教科書」編集長 岡本恵典
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
【出ない？】SPIの図形問題とは？
就活生くん
そもそもSPIの図形問題はどんな問題か分かりません。
では、まずSPIの図形問題の特徴をざっくり解説していきますね！
「就活の教科書」編集部 平井
難易度は小学校～中学校数学レベル
SPIの図形問題の難易度は、小学校～中学校数学レベルです。
問題を解くために使う公式などは、ほとんどが中学校数学までで習っています。
そのため、SPIの図形問題の難易度はそこまで高くありません。
ただし、公式は知っていても、どこで使うか分からないと問題は解けないので注意しましょう。
公式は誰もが知っているので、公式をどう使うかが大切です！
「就活の教科書」編集部 平井
SPIでの図形の問題の出題頻度は低い
SPIでの図形の問題の出題頻度は「低い」と言えます。
能力検査の中で図形の問題が出題されることは稀にありますが、少ないと言えます。
そもそも、SPIの出題範囲に図形という分野があるわけではありません。
様々な分野の問題に図形が使われているというだけです。
なので、対策の優先順位は低いです。
頻出分野である損益算や推論の対策が終わってない人は、そちらを対策しましょう。
SPIの能力検査の「頻出問題が知りたい！」という人は、以下の記事も併せて読んでみてください。
「就活の教科書」編集部 平井
SPIの図形問題は対策すれば難しくない
SPIの図形問題は、対策すれば解けるようになります。
なぜなら、使う公式は中学校までで習っているからです。
例えば、三角形の面積、平行四辺形の面積などです。
なので、図形問題の解き方自体は難しくはないです。
ただし、慣れていないと図形問題は難しく感じるでしょう。
頻出分野の対策ができているなら、図形問題も対策しておきたいところです。
SPIの高得点の目安や、企業のボーダーラインが知りたい就活生は、以下の記事も併せて読んでください！
「就活の教科書」編集部 平井
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
【解き方も解説】SPIの図形問題の例題と解説5選
就活生ちゃん
図形問題の対策がしたいので、例題が知りたいです！
分かりました。
では、図形問題の例題を5つ、紹介します。
「就活の教科書」編集部 平井
- 例題①：図形の面積
- 例題②：長方形の面積を用いた問題
- 例題③：長方形の面積の応用問題
- 例題④：円の面積を用いた問題
- 例題⑤：図形を使った解法
例題①：塗り分け問題
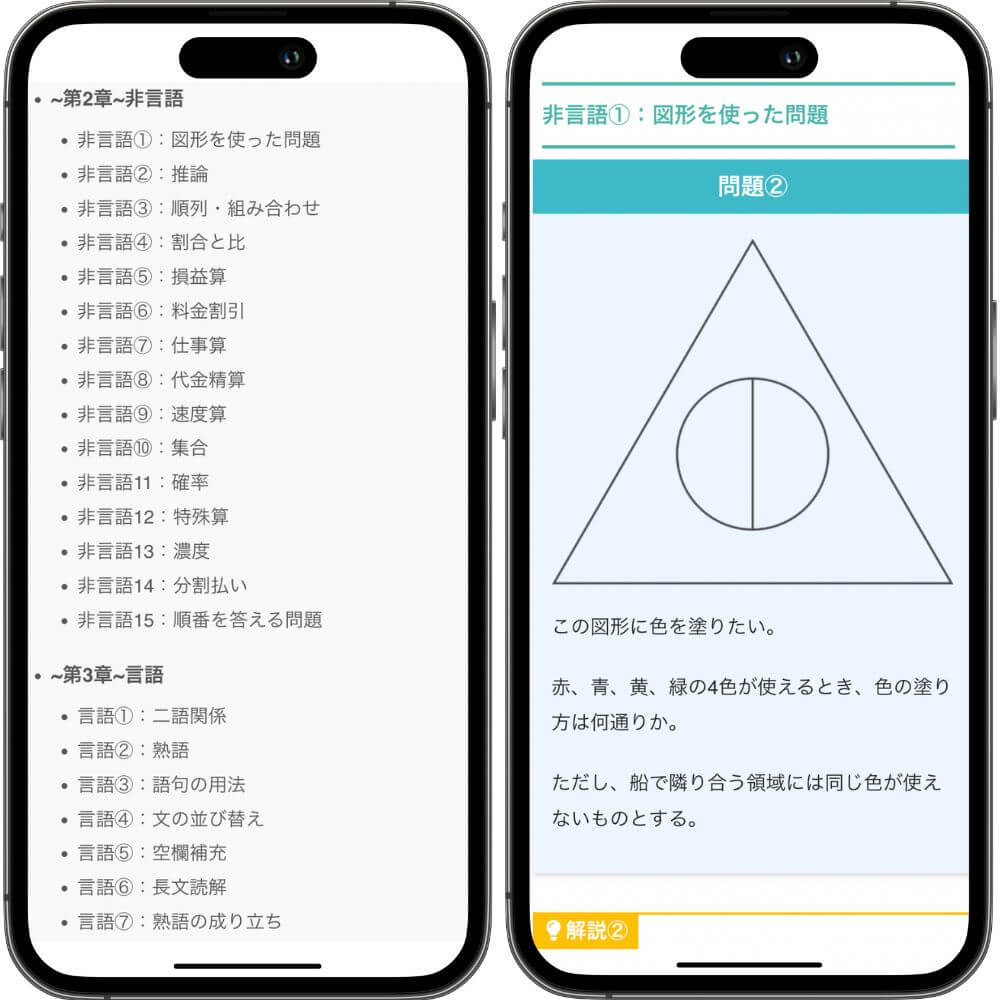
この図形に色を塗りたい。
赤、青、黄、緑の4色が使えるとき、色の塗り方は何通りか。
ただし、船で隣り合う領域には同じ色が使えないものとする。
【解答】
24通り
【解説】
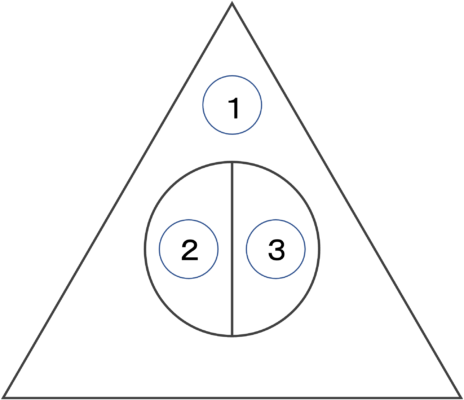
①に塗る色は4色のうち1色なので、4通り。
すると、②に塗る色は残りの3色から1色なので、3通り。
すると、③に塗る色は残りの2色から1色なので、2通り。
したがって、4×3×2=24通り
「別解」
4色から3色を選んで、図の①、②、③の3カ所に色を塗るので、
4P3=24通り
例題②：グラフの領域
次の3つの指揮によって示される放物線と直線は、下図のように平面を8つの領域で分ける。
- ア：y=x^2
- イ：y=x+2
- ウ：y=0
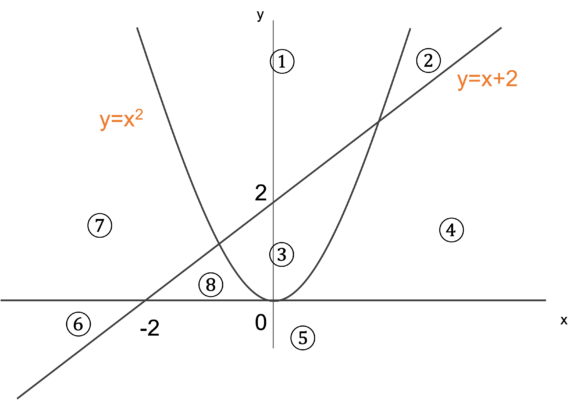
次の2式からなる連立不等式で表される領域はどれか。
- カ：y>x^2
- キ：y<x+2
【解答】
③
【解説】
不等式がyに対して開いていれば、yの値の方が大きいので、上の領域。
不等式がyに対して閉じていれば、yの値の方が小さいので、下の領域。
すると、y>x^2の範囲は以下の通り。
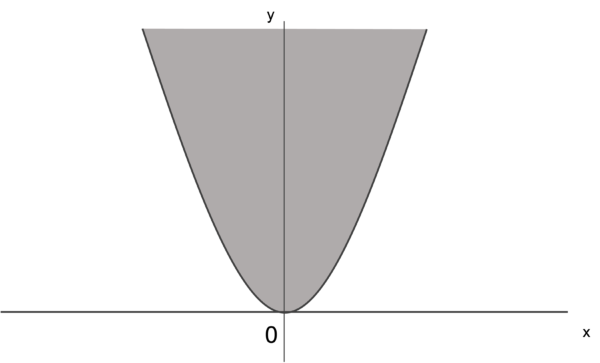
また、y<x+2の範囲は以下の通り。
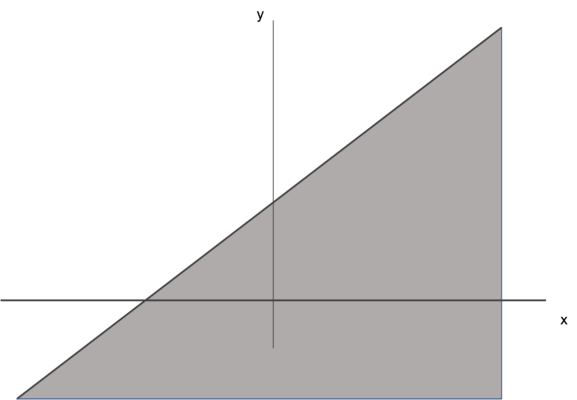
これら2つの領域が重なっている部分が求める領域なので、③
「SPIやWebテストの問題をもっと練習したい！」という方は、SPI頻出問題集を使うのがおすすめです。
SPI頻出問題集は、非言語・言語のよく出る問題を網羅しており、効率よく最短でSPIやWebテストの得点アップが狙えますよ。
就活アドバイザー 京香
例題③：べん図を使って解く問題（集合）
外国人200人にアンケートを行ったところ、英語が話せる人は120人、フランス語が話せる人は40人、ドイツ語が話せる人は60人いた。
英語とフランス語の両方が話せる人が25人いた。
英語とフランス語のどちらか片方だけ話せる人は何人か。
ただし、ドイツ語は関係ないものとする。
【解答】
110人
【解説】
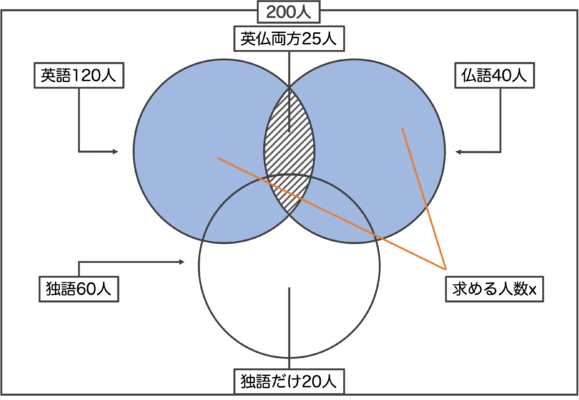
英語と仏語の両方が話せる25人は斜線部分。
求める「英語と仏語のどちらか片方だけ話せる人」は上図の青い部分。
英語だけ→12-25=95人
仏語だけ→40-25=15人
合計 →95+15=110人
例題④：表が出てくる問題（推論）
P市、Q市、R市の人口密度（1km^2あたりの人口）を下表に示してある。
P市とR市の面積は等しく、Q市の面積はP市の2倍である。
| 市 | 人口密度 |
|---|---|
| P | 390 |
| Q | 270 |
| R | 465 |
次の推論ア、イの正誤を考えなさい。
- ア：Q市とR市を合わせた地域の地域の人口密度は300である
- イ：Q市の人口はR市の人口より多い
【解答】
推論ア：誤り
推論イ：正しい
「P市とR市の面積は等しく、Q市の面積はP市の2倍」なので、
仮にP市とR市の面積を1km^2、Q市の面積を2km^2と考える。
アについて、
Q市の人口は、270×2=540人
R市の人口は、465×1=465人
2つの死を合わせた地域の面積は3km^2なので、人口密度は、
（540+465）÷3=335
になるので、300ではない。
よって、アは誤り。
イについて、
Q市の人口は540人、R市は465人なので、Q市の方が多い。
よって、イは正しい。
例題⑤：法則性（WEB-CABから）
空欄に当てはまる選択肢を1つ選び、図形群の法則性を完成させなさい。
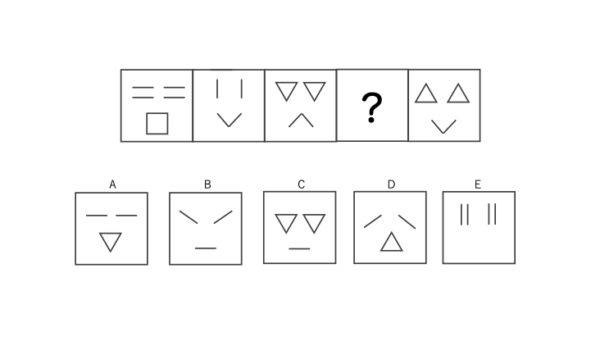
【解答】
E
【解説】
左から右に考える
法則性：図形を構成する線の数が「8本⇄4本」を繰り返す
今回参考にした問題集
また、今回の問題は、以下の問題集を参考に作成しました。
たくさんの問題が掲載されているので、もっと問題を解きたい人にはおすすめです。
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
【短期間でできる】SPIやその他のWebテスト選考を通過するための対策法
就活生くん
SPIや玉手箱、その他のWebテストをいろんな企業の選考で受けないといけないのですが、SPI対策以外にもESや面接などに時間を使いたいです。
短期間で合格ラインまで持っていけるような対策法はないのでしょうか？
短期間でSPIやWebテストの対策をして選考にサクッと通過できるようにしたい就活生は多いです。
そこでここでは、短期間でできるSPIやその他のWebテスト選考を通過するための対策法を紹介しますね。
先に結論を伝えておくと、SPIやWebテストの良く出る問題を練習しておくのが一番おすすめですね！
就活アドバイザー 京香
- 対策法：SPIやWebテストのよく出る問題を練習しておく
- 対策法：性格テストの模擬練習をしておく
- 対策法：SPI対策本を買って苦手分野の問題に取り組む
それでは、それぞれ解説していきます。
就活アドバイザー 京香
対策法：SPIやWebテストのよく出る問題を練習しておく
短期間でできるSPIやその他のWebテスト選考を通過するための対策法は「SPIやWebテストのよく出る問題を練習しておく」ことです。
SPIや玉手箱、Webテストでは、毎回似たような問題が数多く出題されるため、頻出問題だけでも勉強しておくことで合格ラインを越えられることが多いです。
そこで問題をたくさん練習したい方は、SPIやWebテストの問題を網羅した「SPI頻出問題集」を使うのがおすすめです。
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
\ 140,000人以上が利用中！ /
SPIの練習問題を解く
（SPI頻出問題集）
＊公式LINE限定で無料配布中！
SPI頻出問題集は「実際の問題と類似してる点が多く、非常に役立ちました。」という非常に信頼性の高い口コミがありますよ。
就活アドバイザー 京香
対策法：性格テストの模擬練習をしておく
短期間でできるSPIやその他のWebテスト選考を通過するための対策法は「性格テストの模擬練習をしておく」ことです。
実は就活生にはあまり知られていないですが、SPIやWebテストでは性格検査で落ちることがよくあります。
言語や非言語の問題だけを対策していると、性格テストで落ちることになってしまうため、性格テストの対策もする必要があります。
そこでおすすめなのが、本番同様にSPIの性格テストを体験できる「適性診断AnalyzeU+」です。
- 251問の質問があるのでSPIやWebテストの性格検査の対策に向いている
- 100万人のデータから診断してくれるのでかなり正確な結果がわかる
- ついでに診断結果からあなたにおすすめの職種もわかる
\ 大手,優良企業からスカウトが届く! /
客観的な性格診断を受ける
（適性診断AnalyzeU+）
＊プロフィール登録で優良企業のスカウトGET！
適性診断AnalyzeU+は「SPIの性格検査以外にもちゃんと自分の強みがわかる」という点で非常に就活生からの評価が高い診断ですよ。
就活アドバイザー 京香
対策法：SPI対策本を買って苦手分野の問題に取り組む
短期間でできるSPIやその他のWebテスト選考を通過するための対策法は「SPI対策本を買って苦手分野の問題に取り組む」ことです。
SPIの対策本には、どのように対策すべきかやどんな問題が出題されるのかが詳しくまとめられています。
そのため、しっかりと対策したい方にはSPIの参考書をおすすめします。
SPIの問題集を反復して解くうちに、SPIの問題形式になれることが出来ます。
解く時にはしっかりと時間を計測して練習しましょうね。
就活アドバイザー 京香
SPI/テストセンターについて悩んでいる人にオススメの記事一覧
「SPI対策方法が分からない」「SPI対策をしたい」という人には以下の記事がおすすめです。
SPIの能力検査と性格検査対策方法について知れ、選考通過率がアップするので、合わせて読んでみてください。
就活アドバイザー 京香
合格ラインに関する記事
⇒【SPIテストセンター】企業別のボーダー/合格ライン一覧表
能力検査対策に関する記事
⇒【判別URLも】Webテスト22種類の見分け方
⇒【完全版】SPIテストセンターの対策方法とコツ
⇒【無料版も】SPI/適性検査対策アプリおすすめ11選
⇒【頻出問題も】SPIの出題範囲（非言語/言語）を解説
性格検査対策に関する記事
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
SPIの図形問題のコツや対策法
就活生くん
図形問題のコツや対策法が知りたいです！
分かりました。
では、図形問題のコツを3つ、紹介します。
「就活の教科書」編集部 平井
- コツ①：多くの練習問題を解きパターンを覚える
- コツ②：図形ごとの公式を暗記しておく
- コツ③：解くスピードを上げる
コツ①：多くの練習問題を解きパターンを覚える
SPIの図形問題を解くときのコツ1つ目は、「多くの練習問題を解きパターンを覚える」です。
図形問題の公式はいくつもあるので、「どの公式を使うのか」を見極める必要があります。
そのために、多くの練習問題を解いて、問題のパターンを覚えましょう。
使う公式は基本的なものばかりなので、パターンが分かれば解きやすくなります。
「SPIの図形問題を無料でたくさん練習したい！」という就活生に向けて、SPIを無料で解けるサイトを以下の記事にまとめました。
ぜひ参考にしてみてください。
「就活の教科書」編集部 平井
コツ②：図形ごとの公式を暗記しておく
SPIの図形問題を解くときのコツ2つ目は、「図形ごとの公式を暗記しておく」です。
図形問題は、図形の長さや面積を求める問題です。
したがって、公式を覚えていなければ解くことができません。
なので、図形ごとの公式は暗記しておきましょう。
中学校数学までで習っているはずなので、今は忘れていても、すぐに覚えられます。
コツ③：解くスピードを上げる
SPIの図形問題を解くときのコツ3つ目は、「解くスピードを上げる」です。
問題を解くスピードを上げることで、時間に余裕を作ることができます。
時間に余裕があると、焦ってミスをしてしまうことが無くなります。
そのため、問題を解くスピードを上げるようにしましょう。
図形問題の難易度は低めなので、慣れれば早く解けるようになります。
また、図形問題に限らず、SPIは時間との勝負です。
図形問題に使う時間を短縮できれば、難しい推論問題などに時間を使うことができます。
つまり、図形問題を解くスピードを上げることは、SPI全体の対策になります。
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
SPIの図形問題で覚えるべき公式一覧
就活生ちゃん
SPIの図形問題を解くためには、どの公式を覚えておくべきですか？
図形問題では、基本的な図形の公式はすべて覚えておきましょう！
具体的には以下の公式です。
「就活の教科書」編集部 平井
- 三角形の面積＝底辺×高さ÷2
- 四角形の面積＝底辺×高さ
- 平行四辺形の面積＝底辺×高さ
- 台形の面積＝(上底+下底)×高さ÷2
- 円の面積＝半径×半径×π
- 扇形の面積＝半径×半径×π×中心角÷360
- 円周の長さ＝直径×π
また、図形の性質も覚えておくべきです。
図形には以下のような性質があります。
「就活の教科書」編集部 平井
- 三角形の内角の和＝180°
- 四角形の内角の和＝360°
- 対頂角は等しい
- 平行な2直線の同位角、錯角は等しい
- 平行な2直線の同側内角の和＝180°
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
SPIの非言語分野が苦手な人におすすめの対策法
就活生くん
図形問題以外にも、SPIの非言語分野全般が苦手です・・・
どんな対策をすればよいですか？
文系の就活生の中には、非言語分野が苦手な人はたくさんいます。
そこで、SPIの非言語分野が苦手な人におすすめの対策法を2つ紹介します。
「就活の教科書」編集部 平井
- 対策法①：SPIの問題集を解く
- 対策法②：SPIのアプリを利用する
対策法①：SPIの問題集を解く
SPI非言語分野が苦手な人におすすめの対策法1つ目は、「SPIの問題集を解く」です。
SPIの問題集を反復して解くうちに、SPIの問題形式に慣れることが出来ます。
問題に慣れることで、問題のパターンが分かる上、解くスピードも速くなります。
また、、実戦形式の問題集を解くことで、時間配分が上手にもなります。
そして問題に慣れるには問題集を繰り返し解くことが効果的です。
1冊の問題を繰り返し解くと、問題パターンごとの解き方を効率よく身に付けられるので、おすすめです。
「どの問題集を使えばいいか分からない」という人は以下の記事も読んでみてください！
「就活の教科書」編集部 平井
対策法②：SPIのアプリを利用する
SPI非言語分野問題が苦手な人におすすめの対策法2つ目は、「SPIのアプリを使う」です。
SPI言語・非言語 一問一答は、SPI対策を効率よくすることが出来るスマホアプリです。
SPI言語・非言語 一問一答のメリットは以下の通りです。
- 総問題数は300問以上あるからしっかり練習できる
- 間違えた問題は自動でチェックしてくれるから、復習も簡単
- モード切替で効率的に学べるから、1つのアプリで網羅したい人にぴったり
自分に合わせて効率的に学習できるので、1つのアプリで対策したいという人におすすめです。
スキマ時間でどんどん問題を解きましょう！
「就活の教科書」編集部 平井
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
SPIの図形問題に関するよくある質問
最後に、SPIの図形問題に関するよくある質問に回答していきます！
「就活の教科書」編集部 平井
- 質問①：SPIの図形問題は、捨ててもいいの？
- 質問②：SPIの図形問題は、他の単元よりも難しいの？
- 質問③：SPIの図形問題は、規則性があるの？
質問①：SPIの図形問題は、捨ててもいいの？
SPIの図形問題に関するよくある質問1つ目は、「SPIの図形問題は、捨ててもいいの？」です。
SPIの図形問題は「捨てる選択肢もアリ」です。
図形問題は、頻出分野では無いので、対策の優先順位は低いです。
なので、推論やほかの頻出分野の対策ができていないなら、図形問題は捨てても良いでしょう。
ただし、「どんな問題が来ても解けるようにしたい！」という方は、図形問題も一度対策をしておくと良いです。
質問②：SPIの図形問題は、他の単元よりも難しいの？
SPIの図形問題に関するよくある質問2つ目は、「SPIの図形問題は、他の単元よりも難しいの？」です。
図形問題の難易度は、小学校～中学校数学レベルです。
中学数学までの知識があれば解けるので、特別難しい問題ではないです。
したがって、他の分野と同程度の難易度と言えます。
でも、「図形問題がとても苦手・・・」という人もいますよね。
そんな人は、一度は対策した方が良いかもしれません。
「就活の教科書」編集部 平井
質問③：SPIの図形問題は、規則性があるの？
SPIの図形問題に関するよくある質問2つ目は、「SPIの図形問題は、規則性があるの？」です。
図形問題には、ある程度規則性があると言えます。
なぜなら、使う公式は限られていて、パターンが多くないからです。
例えば、問題に使われている図形が長方形と三角形だけのとき、急に円の面積公式を使うことはまずありません。
なので、図形問題には規則性があり、繰り返し問題を解くことで対策できます。
また、SPI非言語には図形問題以外にも様々な問題があります。
SPI非言語の他の問題については以下の記事で詳しく解説しているので、ぜひ読んでみてください
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
まとめ：SPIの図形問題を完璧にして、高得点を目指そう
いかがだったでしょうか。
この記事では、「SPIの図形問題」について徹底解説しました。
併せて、「SPIの図形問題の例題」や「図形問題で覚えておくべき公式」も紹介しました。
この記事が、少しでも就活生の皆さんの参考になれば幸いです。
最後のこの記事を簡単にまとめておきます。
◆【特徴を解説】SPIの図形問題とは？
- 難易度は小学校～中学校数学レベル
- SPIでの図形の問題の出題頻度は？
- SPIの図形問題は対策すれば難しくない
◆【解き方も解説】SPIの図形問題の例題と解説5選
- 例題①：図形の面積
- 例題②：長方形の面積を用いた問題
- 例題③：長方形の面積の応用問題
- 例題④：円の面積を用いた問題
- 例題⑤：図形を使った解法
◆SPIの図形問題のコツや対策法
- コツ①：多くの練習問題を解きパターンを覚える
- コツ②：図形ごとの公式を暗記しておく
- コツ③：解くスピードを上げる
◆SPIの図形問題で覚えるべき公式一覧
◆SPIの非言語分野が苦手な人におすすめの対策法
- 対策法①：SPIの問題集を解く
- 対策法②：SPIのアプリを利用する
◆SPIの図形問題に関するよくある質問
- 質問①：SPIの図形問題は、捨ててもいいの？
- 質問②：SPIの図形問題は、他の単元よりも難しいの？
- 質問③：SPIの図形問題は、規則性があるの？
◆まとめ：SPIの図形問題を完璧にして、高得点を目指そう