- SPI推論は出題範囲の中で難易度が高い
- SPI推論はどのテスト形式でも必ず出る頻出問題
- 【10題】SPI推論の問題例と解き方
➔問題を解いてみる - SPI推論は高得点のためには必須！
-
Webテスト（SPI,玉手箱など）の対策には、以下のツールがおすすめ
-
【就活生/転職者】SPI頻出問題集（LINEで無料配布）
（SPI/Webテストの頻出問題を練習） -
【就活生】Lognavi WEBテスト
（言語・非言語118問,性格診断90問） -
【就活生】適性診断AnalyzeU+
（251問で性格診断）
-
【就活生/転職者】SPI頻出問題集（LINEで無料配布）
この記事では、SPIの「推論」の練習問題の解き方を解説します。 あわせて、SPIの推論の解き方のコツや対策方法を紹介しているので、ぜひ参考にしてみてください。
ちなみに、「SPIやテストセンターで落ちたくない」「Webテストを効率的に勉強したい」という人は、SPIやWebテストの例題を短時間で練習できる「SPI頻出問題集（公式LINEで無料配布）」などのサービスを活用しましょう。 この記事を読めば、SPIの推論について理解が深まり対策の仕方がわかります。 「SPI推論の問題が難しいと感じる就活生」や、「SPI推論の問題や解き方のコツが知りたい就活生」はぜひ最後まで読んでください。
「SPIなどのWebテストで落とされたくない！」という方には「SPI頻出問題集」で本番の問題に近い練習をして、効率良く得点をUPさせるのがおすすめです。
ちなみに「SPI頻出問題集」以外にも、SPI模擬テストが受けられる「Lognavi WEBテスト」、251問の性格診断「適性診断AnalyzeU+」もおすすめですよ。
就活アドバイザー 京香
- 【就活生/転職者】SPI頻出問題集（公式LINEで無料配布）
【公式サイト】https://reashu.com/linelp-spi/
- Webテストで頻出の問題がわかる
- 【就活生】Lognavi WEBテスト（言語・非言語118問,性格90問）
【公式サイト】https://lognavi.com/
- 自分の実力を客観的に知れる
- 【就活生】適性診断AnalyzeU+（全251問、客観的な性格診断）
【公式サイト】https://offerbox.jp/
- 診断でSPI性格検査の練習も
「結局どのサービスを使えば良いかわからない…」という方は「SPI頻出問題集」で練習問題を解いてみるのが一番おすすめですよ。
就活アドバイザー 京香
目次
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
【難しい？】SPIの推論は難易度が高く、高得点のために重要な問題
皆さん、こんにちは。「就活の教科書」編集部の平井です。
この記事では、「SPIの推論」について徹底解説していきます。
「就活の教科書」編集部 平井
就活生くん
SPIの推論の問題は、どんな特徴があるんですか？
平井さん、教えてください！
わかりました！
それでは、SPIの推論問題の特徴を解説していきます！
「就活の教科書」編集部 平井
SPI推論は高頻出問題なので対策すべき
SPI推論の問題の特徴は、「SPIの中で難易度が高く、かつ高頻出で重要な問題」です。
制限時間の中で、与えられた情報をもとに正しい結論を推測する必要があるため、特に難易度の高い問題です。
SPIには、「テストセンター」「ペーパーテスト」「Webテスティング」の3つの受験方式があり、出題範囲も変わりますが、推論は3つのどの形式でも、必ず出題されます。
以下にSPI推論の特徴を記載します。
- SPIの出題範囲の中でも難易度の高い問題
- 複雑な計算、特別な前提知識が必要ない
- SPI非言語で高得点を取るには、推論問題が占める割合が大きい
- ペーパーテストの場合、30問のうち7問以上は推論の問題が出題される
推論はSPIの出題範囲の中でも難易度が高いです。
また、多くの人が推論の問題に慣れていないため、問題を解くのにも時間がかかります。
なので、SPI推論の問題を難しいと感じているのは、あなただけではありません。
SPIの受験方式による違いを詳しく知りたい方は下の記事を読んでみてください。
出題範囲だけでなく、制限時間や問題数についても解説しています。
「就活の教科書」編集部 平井
SPI推論は、コツをつかめば意外と解ける！
SPI推論に難しさを感じる人は多いですが、コツをつかめば意外と解ける問題でもあります。
特殊な公式の暗記などを必要としないからです。
コツをつかむには、様々な問題に触れ、「推論」の種類をつかむことが重要です。
このあと、種類別にSPI推論の問題例を紹介していきます！
就活アドバイザー 京香
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
【高得点を取る】SPI推論の頻出問題10パターンと解き方
就活生ちゃん
SPI推論には、どんな問題が出るんですか？
また、問題の解き方も教えてください！
わかりました！
では、SPI推論の問題例と解き方を紹介していきます！
「就活の教科書」編集部 平井
- SPI推論の問題例①：順序
- SPI推論の問題例②：密度
- SPI推論の問題例③：発言の正誤
- SPI推論の問題例④：対戦（リーグ戦）
- SPI推論の問題例⑤：対戦（トーナメント戦）
- SPI推論の問題例⑥：位置
- SPI推論の問題例⑦：平均
- SPI推論の問題例⑧：内訳
- SPI推論の問題例⑨：整数
- SPI推論の問題例⑩：割合
SPI推論の問題例①：順序
SPI推論の問題例の1つ目は、「順序」です。
順序の問題は、与えられた情報から想定できる順序を導き、正しい推論を選択する問題です。
順序の問題を解くときは、想定できる順序のパターンをすべて書き出すことがポイントです。
P、Q、R、S、Tの5つの支店の売上高を比較した。
5つの支店について次のことが分かっている。
- ⅰ）Rの売上高は、Sより上である
- ⅱ）Tの売上高は、Rよりも上だが、1位ではなかった
- ⅲ）Qの売上高は、Pより上である
- ⅳ）同じ売上高の支店はない
次のア、イ、ウの推論のうち、必ず正しいものはどれか。
- ア Qの売上高は1位である
- イ Sの売上高は5位である
- ウ 2位はPまたはTである
| A：アだけ |
| B：イだけ |
| C：ウだけ |
| D：アとイの両方 |
| E：アとウの両方 |
| F：イとウの両方 |
| G：アとイとウのすべて |
| H：必ず正しい推論はない |
解答
E： アとウの両方
解説
順位を推論する問題は、想定できる順位のパターンを全て洗い出す。
下記のルールにしたがって、与えられた情報を図式化する。
「順位の高低関係のみ」を表現するときは、「[ 順位がより高い方 ] > [ 順位がより低い方 ]」と表す。
「連続する順位の並び」を表現するときは、「[ 順位が高い方 ] → [ 順位が低い方 ]」と表す。（ただし、この問題では使わない。）
このルールにしたがって、問題文の情報を図式化する。
ⅰ）「Rの順位は、Sより上である」より、RとSの順位関係は、「R > S」・・・①
ⅱ）「Tの順位は、Rよりも上だが、1着ではなかった」より、TとRの順位関係は、「□ > T > R」・・・②
①、②より、「□ > T > R > S」・・・③
ⅲ）「Qの順位は、Pより上である」より、「Q > P」・・・④
③、④より、考えられる順位は、次の4通りである。
| 順位 | |||||
| 1位 | 2位 | 3位 | 4位 | 5位 | |
| パターン1 | Q | P | T | R | S |
| パターン2 | Q | T | P | R | S |
| パターン3 | Q | T | R | P | S |
| パターン4 | Q | T | R | S | P |
ここで、推論ア～ウについて考えると
表より、1位はQである。よって、ア「Qは1位である」は必ず正しい。
表より、5位はSかPである。よって、イ「Sは5位である」は正しいとは限らない。
表より、2位はPまたはTである。よって、ウ「2位はPまたはTである」は必ず正しい。
したがって、正しい推論はアとウの両方。
SPI推論の問題例②：密度
SPI推論の問題例の2つ目は、「密度」です。
密度の問題は、与えられた密度の情報から、正しい推論を選んだり、異なる条件の密度を計算する問題です。
多くの場合、密度に加えて、「2倍」や「半分」などの比率に関する情報が与えられています。
密度の問題を解くときは、計算しやすくするために、簡単な数値を当てはめましょう。
A市、B市、C市の人口密度（面積1km2当たりの人口）は下表の通りである。
A市とB市の面積は等しく、それぞれC市の面積の半分である。
| 市 | 人口密度 |
| A | 200 |
| B | 160 |
| C | 120 |
次のア、イの正誤を考え、AからIまでの中から正しいものを1つ選びなさい。
- ア：A市の人口はC市より少ない
- イ：B市とC市を合わせた人口密度はA市の人口密度と等しい。
- アもイも正しい
- アは正しいが、イは分からない
- アは正しいが、イは誤り
- アは分からないが、イは正しい
- アもイも分からない
- アは分からないが、イは誤り
- アは誤りだが、イは正しい
- アは誤りだが、イは分からない
- アもイも誤り
解答
C . アは正しいが、イは誤り
解説
面積を仮定して、それぞれの市の人口を計算していきましょう。
A市とB市の面積は等しく、それぞれC市の面積の半分であることから、
A市の面積を1 km2と仮定すると、B市の面積は1 km2、C市の面積は2 km2となります。
それぞれの市の人口は、
A市の人口：200 × 1 = 200 人
B市の人口：160 × 1 = 160 人
C市の人口：120 × 2 = 240 人
(アについて)
A市の人口200人は、C市の人口240人よりも少ないので、記述は正しいです。
(イについて)
B市とC市を合わせた人口は、160 + 240 = 400 人
B市とC市を合わせた面積は、1 + 2 = 3 km2
よって、B市とC市を合わせた人口密度は、400 / 3 = 133.3 人/ km2
したがって、A市の人口密度200人/ km2より少ないため、記述は誤りです。
「SPIやWebテストの問題をもっと練習したい！」という方は、SPI頻出問題集を使うのがおすすめです。
SPI頻出問題集は、非言語・言語のよく出る問題を網羅しており、効率よく最短でSPIやWebテストの得点アップが狙えますよ。
就活アドバイザー 京香
SPI推論の問題例③：発言の正誤
SPI推論の問題例の3つ目は、「発言の正誤」です。
発言の正誤の問題は、不確実な発言がいくつか与えられ、お互いの発言の関係性として、正しいものを選ぶ問題です。
発言の正誤の問題を解くときは、それぞれの発言の関係性をすべて洗い出しましょう。
ジョーカーを含まない52枚1組のトランプから、カードが1枚配られた。
この1枚のカードについて、A、B、Cの3人から次の発言があった。
- Aさん）このカードは、ハートの8ではなかった。
- Bさん）このカードは、ハートではなかった。
- Cさん）このカードは、スペードの8であった。
3人の発言は信頼できるとは限らない。そこで、いろいろな場合を想定して推論がなされた。
（1）次のア、イ、ウの推論のうち、正しいのはどれか。
- ア：Aさんが正しければ、Bさんも必ず正しい
- イ：Bさんが正しければ、Cさんも必ず正しい
- ウ：Cさんが正しければ、Aさんも必ず正しい
- アだけ
- イだけ
- ウだけ
- アとイの両方
- アとウの両方
- イとウの両方
- アとイとウのすべて
- 正しい推論はない
解答
C：ウだけ
解説
ア、イ、ウの推論を順番に検証していきましょう。
- (アについて)「 Aさんが正しければ、Bさんも必ず正しい」
Aさんが正しい場合、カードはハートの8以外の51枚のどれかになります。
例えば、ハートの5や、スペードの10などの場合が考えられます。
Bさんは「ハートではない」と発言していますが、8以外のハートの可能性があるため、必ず正しいとは限りません。
よって、アの推論は誤りです。
- (イについて)「Bさんが正しければ、Cさんも必ず正しい」
Bさんが正しい場合、カードはハート以外のスペード、クローバー、ダイヤのどれかになります。
例えば、スペードの5やダイヤのAなどの場合が考えられます。
Cさんは「スペードの8である」と発言していますが、Bさんの発言からは、必ず「スペードの8」であるとは言えません。
よって、イの推論は誤りです。
- (ウについて)「Cさんが正しければ、Aさんも必ず正しい」
Cさんが正しい場合、このカードはスペードの8の1つに特定されています。
この時、Aさんの「ハートの8ではない」の発言は矛盾がありません。
よって、ウの推論は正しいです。
以上から、ウの推論のみが正しいとするCが正解となります。
SPI推論の問題例④：対戦（リーグ戦）
SPI推論の問題例の4つ目は、「対戦（リーグ戦）」です。
対戦の問題は、与えられた情報から、対戦結果として正しい推論を選ぶ問題です。
対戦の問題を解くときは、与えられた情報を対戦表にまとめてから、選択肢を考察しましょう。
P、Q、R、Sの４チームが、サッカーの試合を総当たり戦で行った。その試合結果について、次のことが分かっている。
- Pは1勝2敗だった
- PはQに勝った
- RはPに勝った
- SはQに勝った
- 引き分けの試合は無かった
次のア、イ、ウの推論のうち、必ずしも誤りとはいえない推論はどれか。
- ア：Qは1勝2敗だった
- イ：Rは全勝だった
- ウ：Sは1勝2敗だった
- アだけ
- イだけ
- ウだけ
- アとイの両方
- アとウの両方
- イとウの両方
- アとイとウのすべて
- 必ずしも誤りとは言えない推論はない
解答
D：アとイの両方
解説
対戦成績の問題では、総当たり戦の表を作成して考えると良いです。
ii) iii) iv) の情報から、対戦表は次のようになります。
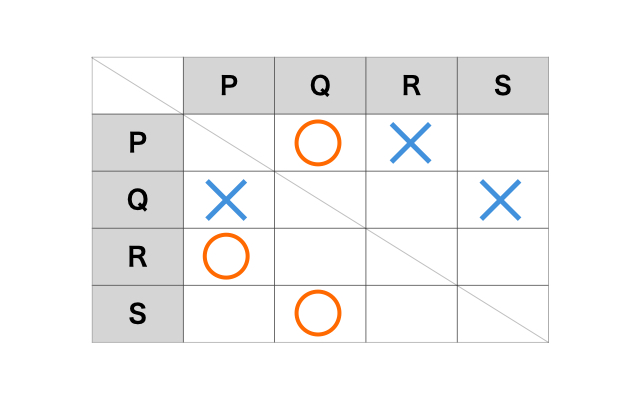
i)で「Pは1勝2敗である」ので、PはSに負けたことがわかります。
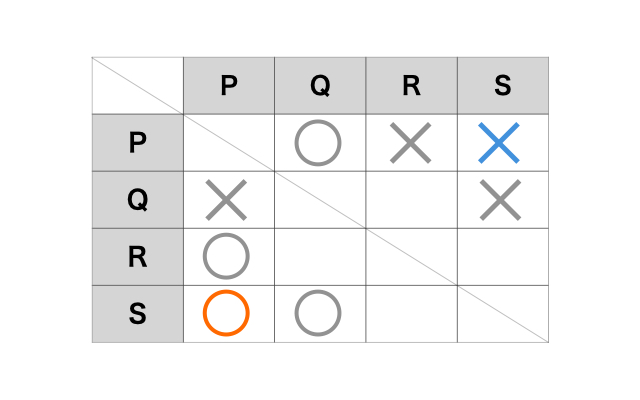
i) ~ iv)の情報から分かることは、ここまでです。
この状態でv)を満たすように空欄を埋めたときに、ア、イ、ウのそれぞれが成り立つ場合があるかを検証していきましょう。
- (アについて）「Qは1勝2敗だった」
QがRに勝った場合には、アの推論は正しくなります。
- (イについて)「Rは全勝だった」
RがQとSの両方に勝った場合に、イの推論は正しくなります。
- (ウについて)「Sは1勝2敗だった」
Sは既に2勝しているので、SとRの結果によらず、ウの推論は誤りです。
以上から、アとイの両方が正しいとしているDが正解となります。
SPI推論の問題例⑤：対戦（トーナメント戦）
SPI推論の問題例の5つ目は、「対戦（トーナメント戦）」です。
対戦には、先ほどの総当たり戦とは別にトーナメント戦の場合もあります。
トーナメント戦の際には、トーナメント表を書き、分かっている情報を書き込んでいくことがポイントです。
A、B、C、D、E、F、G、Hの8チームがトーナメント方式でバスケットボール大会に臨んだ。対戦の詳細は以下の通りです。
Ⅰ BはD、F、Hと対戦したが、戦った順番はわからない。
Ⅱ Cが2回戦で対戦する可能性があったのはE、Fである。
Ⅲ Cが1回戦で対戦したのは、Aではない。
Cが1回戦で対戦したのはどのチームか、次の選択肢から選びなさい。
- A
- B
- D
- E
解答
3．D
解説
この問題では、トーナメントの条件を基に、Cがどのチームと1回戦で対戦したかを推論します。
まず、条件ⅠからBが戦ったチーム（D、F、H）をトーナメント図に当てはめます。Bが対戦した順番は不明ですが、Bは3回戦まで進出しており、これらのチームと戦いました。
次に、条件Ⅱから、Cが2回戦で対戦する可能性があったのはEかFです。これにより、Cが1回戦で勝利し、EかFと2回戦で対戦する可能性があったことがわかります。
さらに、条件Ⅲから、Cが1回戦で対戦したのはAではないため、残りの可能性はB、D、Eです。しかし、条件ⅡでCがEと2回戦で対戦する可能性があるため、Cが1回戦でEと対戦することはありません。したがって、Cが1回戦で対戦したのは、BかDのどちらかです。
最後に、Bは条件Ⅰで既にDと戦っているため、Cが1回戦で対戦したチームはDであると推論できます。
したがって、正解は「3. D」です。
SPI推論の問題例⑥：位置
SPI推論の問題例の6つ目は、「位置」です。
位置の問題は、位置関係についての情報から、正しい推論を選ぶ問題です。
位置の問題を解くときは、想定される位置関係のパターンを全て洗い出しましょう。
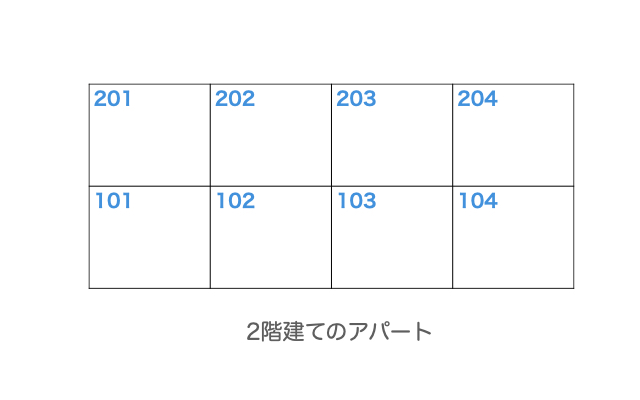
上図のような2階建てのアパートに、A、B、C、D、E、Fの6人が1人1部屋で住んでいて、次のことが分かっている。
- Aは104号室に住んでいる
- Bの真上にはCが住んでいる
- Dの隣のうち、右隣には誰かが住んでいて、左隣は空き室である
- Eの左隣にはFが住んでいる
- Fは端には住んでいない
次のア、イの正誤を考え、AからIまでの中から正しいものを1つ選びなさい。
- ア：Aの真上は空き室である
- イ：Dの右隣にはAが住んでいる
- アもイも正しい
- アは正しいが、イは分からない
- アは正しいが、イは誤り
- アは分からないが、イは正しい
- アもイも分からない
- アは分からないが、イは誤り
- アは誤りだが、イは正しい
- アは誤りだが、イは分からない
- アもイも誤り
解答
G：アは誤りだが、イは正しい
解説
条件を整理しながら、位置を埋めていきましょう。
i) Aは104号室に住んでいる
ii) Bの真上にはCが住んでいる
iv) Eの左隣にはFが住んでいる
の条件を図で整理すると、下のようになります。
ii)やiv)のような、入る場所が分からないが、位置関係が分かるものは、1つのブロックのように扱うと考えやすくなります。
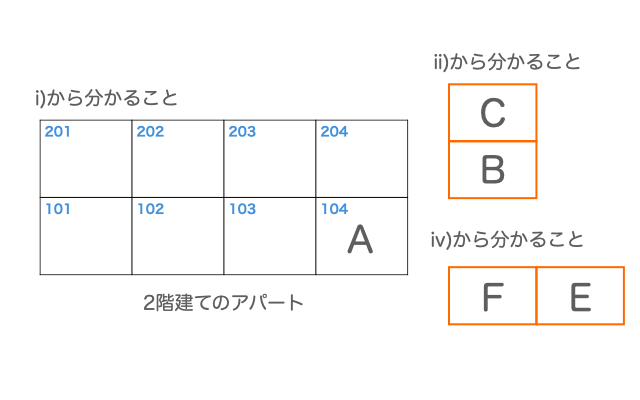
C、Bのブロックの入れ方に着目すると、次の3つのパターンが考えられます。
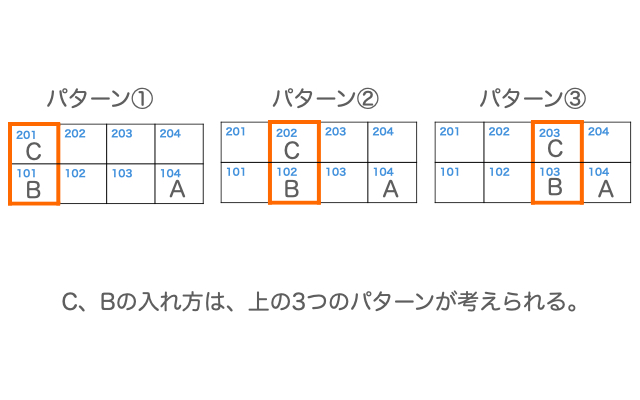
それぞれのパターンについて、F、Eの入れ方、Dの入れ方を考え、条件を満たすかを検証していきます。
パターン①の場合、パターン①-1、パターン①-2が条件を満たします。
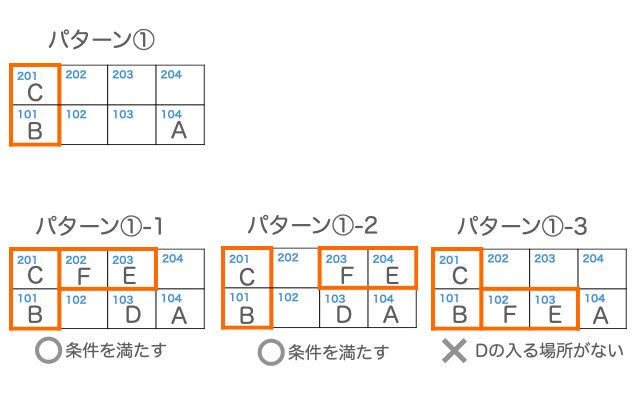
パターン②の場合、iii)の条件を満たすように、Dを入れることができないので、不適となります。
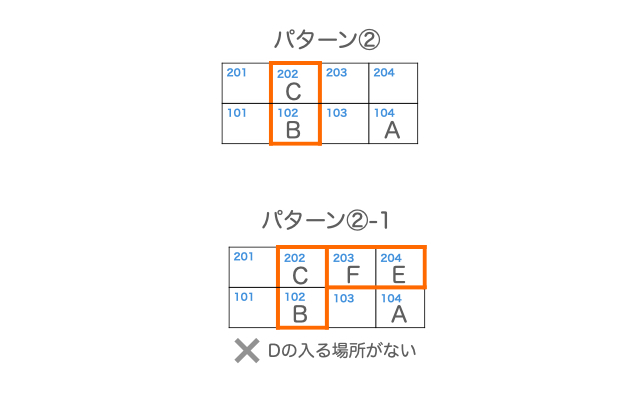
パターン③の場合、v)の条件を満たすように、F、Eを入れることができないので、不適となります。
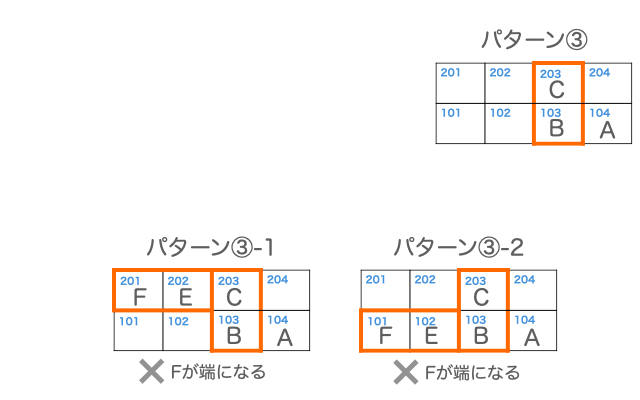
以上から、想定される位置関係は、パターン①-1、パターン①-2のいずれかであることがわかります。
ア) Aの真上は、パターン①-2の場合は、空き家ではないので、推論は誤りです。
イ)Dの右隣は、パターン①-1、パターン①-2のいずれもAなので、推論は正しいです。
したがって、「D：アは誤りだが、イは正しい」が正解となります。
SPI推論の問題例⑦：平均
SPI推論の問題例の7つ目は、「平均」です。
平均の問題は、平均から値段について推測する問題です。
A、B、Cの3つの商品があります。
これらの商品の価格について、次のことがわかっています。
- AとBの価格の平均額は、900円である。
- BとCの価格の平均額は、600円である。
このとき、次のア、イ、ウの推論のうち、必ず正しいものはどれか？
- ア：Bの価格は、Aの価格より高い
- イ：Cの価格は、Aの価格より高い
- ウ：Cの価格は、Bの価格より高い
- アだけ
- イだけ
- ウだけ
- アとイの両方
- アとウの両方
- イとウの両方
- アとイとウのすべて
- 必ず正しい推論はない
解答
H：必ず正しい推論はない
解説
A、B、Cの価格を比較するので、合計値を求めてみます。
「AとBの価格の平均額は、900円である」ので、AとBの価格の合計は
- A + B = 900 × 2 = 1800 ・・・①
「BとCの価格の平均額は、600円である」ので、BとCの価格の合計は、
- B + C = 600 × 2 = 1200 ・・・②
① – ②を考えると、
A – C = 600
となるので、AはCより600円高いことがわかり、Aは600円以上であることが確定します。
ここから、推論を順番に検証します。
(アについて) 「Bの価格は、Aの価格より高い」
AとBの合計が1800円であり、Aが600円以上という条件から、
例えば、Aが1000円、Bが800円の場合、不適となります。
よって、アは誤りです。
(イについて)「Cの価格は、Aの価格より高い」
AはCより600円高いという条件から、CがAより高くなることはありません。
よって、イは誤りです。
(ウについて）「Cの価格は、Bの価格より高い」
例えば、Cの価格を100円とすると、A = 700円、B = 1100円となり、これは式を満たします。
よって、Cの価格がBの価格よりも安い場合もな成り立つので、ウは誤りです。
以上から、「H：必ず正しい推論はない」が正解です・
SPI推論の問題例⑧：内訳
SPI推論の問題例の8つ目は、「内訳」です。
内訳の問題は、与えられた情報から、個数の内訳を推測する問題です。
内訳の問題を解くときは、想定できる個数のパターンを全て書き出しましょう。
青玉、黄玉、赤玉が合わせて7個あります。
それぞれの個数について次のことが分かっています。
- 青玉、黄玉、赤玉は、それぞれ少なくとも1個はある
- 黄玉の数は青玉より少ない
次のア、イ、ウの推論のうち、必ず正しいものはどれか。
- ア：青玉が3個であれば、黄玉は2個である
- イ：黄玉が2個であれば、赤玉は1個である
- ウ：赤玉が3個であれば、青玉は3個である
- アだけ
- イだけ
- ウだけ
- アとイの両方
- アとウの両方
- イとウの両方
- アとイとウのすべて
- 必ず正しい推論はない
解答
C：ウだけ
解説
まず、条件i、iiより、4個の玉の内訳は、次のようになります。
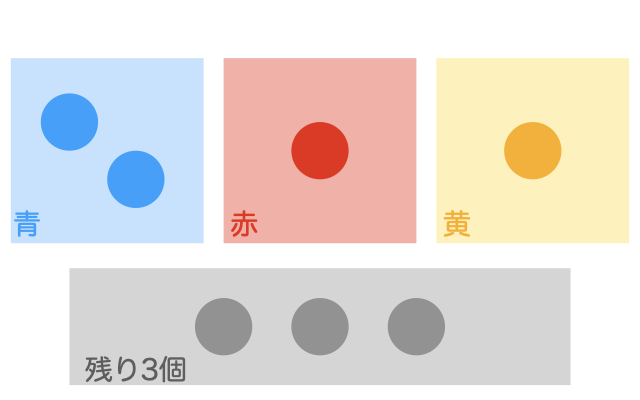
よって、残りの3個の玉の内訳を考えればよいです。
推論を順番に検証していきましょう。
(アについて)「青玉が3個であれば、黄玉は2個である」
黄玉は青玉より少ないので、青玉が3個のとき、黄玉は2個か1個です。
黄玉が1個の場合もあり得るので、アは必ず正しいとは言えません。
(イについて）「黄玉が2個であれば、赤玉は1個である」
黄玉が2個のとき、青玉は3個か4個になります。
青玉が3個のとき、赤玉は2個となるので、イは必ず正しいとは言えません。
(ウについて）「赤玉が3個であれば、青玉は3個である」
赤玉が3個のとき、残る玉は4個ですが、青玉が黄玉よりも多くなる内訳は、青玉3個、黄玉1個の場合のみです。
よって、ウは必ず正しいと言えます。
以上より、「C：ウだけ」が正解です。
SPI推論の問題例⑨：整数
SPI推論の問題例の9つ目は、「整数」です。
整数問題はわからない数字の一つをXとおいて、Xで他の数も表してみることが有効です。
赤、青、緑のボールを合計15個買った。ただし、どのボールも1個以上は買った。それぞれの買った数について、以下のことが分かっている。
Ⅰ 緑のボールは7個以下である。
Ⅱ 赤のボールは青のボールより3個だけ少ない。
青のボールと緑のボールの個数差が3個のとき、赤のボールと緑のボールの差は何個か。
解答
2個
解説
まず、赤のボールが青のボールより3個少ないので、青のボールを x個とすると、赤のボールの数は x−3個になります。
これにより、赤と青のボールの合計は (x−3)+x=2x−3 個になります。
次に、緑のボールの数は全体の合計から赤と青のボールの数を引いたものになりますので、
緑のボールの数は 15−(2x−3)=18−2x個になります。
また、条件Ⅰから、緑のボールの数は7個以下であるため、
この不等式を解くと、
5.5≤x≤8.5
したがって、青のボール xの値は整数なので、 x=6,7, となります。
青と緑のボールの差が3個であるとき、次のケースが考えられます。
- 青: 6 個、赤: 3個、緑: 7個
- 青: 7個、赤: 4個、緑: 6個
- 青: 8個、赤: 5個、緑: 5個
この中で青と緑の差が3個となるのは、青が7個で緑が4個のケースです。
したがって、この場合、赤のボールと緑のボールの差は 4−6=2個です。
SPI推論の問題例⑩：割合
SPI推論の問題例の10つ目は、「割合」です。
割合でも、一つの数字をXとおき、そのほかの数字をXを用いて表すことがポイントです。
A町、B町、C町という3つの町の歳入のうち地方税が占める割合を次の表に示している。
A町とC町の歳入は等しく、B町の歳入はA町の歳入の半分である。
A町とB町が合併してD町ができる場合、次の推論にあてはまる正しいものを選びなさい。
| 町名 | 地方税の割合 |
|---|---|
| A町 | 28% |
| B町 | 18% |
| C町 | 32% |
推論
D町の歳入のうち地方税が占める割合は25%より大きくなる。
選択肢
A. 正しい
B. どちらとも言えない
C. 誤り
解答
C．誤り
解説
まず、A町の歳入を xとし、B町の歳入を x/2 とします。
A町の地方税の金額は、
0.28x
B町の地方税の金額は、
0.18 × x/2 =0.09x
次に、D町の歳入のうち地方税が占める割合を求めます。D町の歳入はA町とB町の歳入を足したものなので、
D町の総歳入は、
x+x2=1.5x
D町の地方税の総額は、
0.28x+0.09x=0.37x
したがって、D町の地方税の割合は、
0.37x / 1.5x= 0.37 / 1.5≒0.2467
これは約24.67%に相当し、25%よりも小さいため、D町の地方税の割合が25%より大きくなるという推論は誤りです。よって、正解は「C. 誤り」です。
「SPIやWebテストの問題をもっと練習したい！」という方は、SPI頻出問題集を使うのがおすすめです。
SPI頻出問題集は、非言語・言語のよく出る問題を網羅しており、効率よく最短でSPIやWebテストの得点アップが狙えますよ。
就活アドバイザー 京香
今回参考にした問題集
今回の例題は、こちらの問題集を参考にされていただきました。
たくさんの問題が掲載されているので、練習をもっとやりたい人にはおすすめです。
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
SPI推論の簡単な解き方や対策方法,コツ5選
就活生くん
SPI推論の解き方のコツはありますか？
はい、SPI推論には解き方のコツがあります！
今から5つほど紹介します！
「就活の教科書」編集部 平井
- SPI推論の解き方のコツ①：問題をしっかり読む
- SPI推論の解き方のコツ②：図式化して整理する
- SPI推論の解き方のコツ③：設問内容から確実に言えることだけで判断する
- SPI推論の解き方のコツ④：解き方を覚える
- SPI推論の解き方のコツ⑤：過去問や問題集を使って問題に慣れる
SPI推論の解き方のコツ①：問題をしっかり読む
SPI推論の解き方のコツ1つ目は、「問題をしっかり読む」です。
当たり前のことですが、SPI推論では、落ち着いて文章を読むことが大切です。
推論は他の問題に比べ時間に余裕があるので、しっかり問題文を読みましょう。
問題をしっかり読むことで、情報の洩れを防ぎ、正答率を上げることができます。
まずは、正確に問題を読み解くことを意識しましょう。
SPI推論の解き方のコツ②：図式化して整理する
SPI推論の解き方のコツ2つ目は、「図式化して整理する」です。
問題文にはたくさんの条件が書かれているため、頭の中だけで考えるのは無理があります。
そのため、図や記号を使い、条件を整理して書き出しましょう。
図式化して整理することで、必要な条件が整理・可視化され、理解しやすくなります。
また、条件をいちいち問題文から確認する必要が無くなります。
SPI推論の解き方のコツ③：設問内容から確実に言えることだけで判断する
SPI推論の解き方のコツ3つ目は、「設問内容から確実に言えることだけで判断する」です。
SPI推論では、図式化して整理した条件と選択肢を照らし合わせて答えを導きます。
この時、設問の条件から断言できることだけで解答を選んでください。
設問の条件にないことから解答を選んでしまうと、誤答につながります。
もし、整理した条件から答えが出ないなら、条件を勘違いしていないか、条件に漏れがないか確認しましょう。
SPI推論の解き方のコツ④：解き方を覚える
SPI推論の解き方のコツ4つ目は、「解き方を覚える」です。
SPI推論問題は個別の問題に対するアプローチ方法は違っても、似たようなパターンで解ける問題が多いです。
そのため、頻出の問題パターンの解き方は覚えてしまいましょう。
解き方を覚えることで、問題を解くスピードが上がります。
また、見慣れない問題が出たとしても、覚えた解き方を応用することで解ける場合があります。
SPI推論の解き方のコツ⑤：過去問や問題集を使って問題に慣れる
SPI推論の解き方のコツ5つ目は、「過去問や問題集を使って問題に慣れる」です。
SPI推論は初見では難しく感じるでしょうが、解いていくうちに問題のパターンが分かってきます。
問題に慣れることで、問題を解くスピードが上がり、時間に余裕ができます。
また、本番のテストで焦って頭が回らなかったり、全く見たことのない問題にパニックになることを防げます。
問題を解くときは、「本番に近い形でやるために、実戦形式の過去問を使う」、「苦手を克服するために範囲ごとに問題集を解いていく」など、目的を決めて取り組みましょう。
SPI/テストセンターの対策に役立つ記事一覧
「SPI対策方法が分からない」「SPI対策をしたい」という就活生には以下の記事がおすすめです。
以下の記事を読めば、SPIの能力検査と性格検査対策方法について知れ、選考通過率がアップします。
就活アドバイザー 京香
この記事を読めば、URLを見ただけでWebテストの種類を見分けることができるようになり、どんなWebテストにも対応できるようになります。
就活アドバイザー 京香
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
SPI推論は捨てるべき？
就活生ちゃん
SPI推論は難しいし、時間もかかります・・・
推論は捨てて他の問題で高得点を狙うのはダメなんですか？
SPI推論は捨てたらダメなのか気になりますよね！
SPIは捨てるべきか解説していきます！
「就活の教科書」編集部 平井
結論：推論は捨てるべきでない
推論が難しいと感じる人は多いと思います。
「時間ばかりかかるし、いっそ推論は捨てよう・・・」
「推論を飛ばして他の問題で点数を稼げばいいのでは？」
と思う人もいるかもしれません。
ですが、推論は捨てるべきではありません。
理由：推論はSPIで高得点を取るためには必須だから
なぜなら、「推論はSPIで高得点をとるためには必須だから」です。
SPIテストセンターでは、出来が良いと推論の問題数が多くなる仕組みになっています。
実際に、推論が半分以上というのがSPI非言語の高得点の目安になっています。
ペーパーテストやWebテスティングでも推論の重要性は変わりません。
そのため、高得点をとるためには、推論問題で正解することが必須だと言えます。
SPIテストセンターの結果の確認方法が知りたい人や、高得点の目安が知りたい人は板の記事をチェックしてください。
「就活の教科書」編集部 平井
また、「推論を含むSPI非言語全般が苦手・・・」という就活生もいると思います。
以下の記事では、SPIの非言語が壊滅的でもSPIに通過できるのかについて解説していますので、ぜひ読んでみてください。
「就活の教科書」編集部 平井
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
【短期間でできる】SPIやその他のWebテスト選考を通過するための対策法
就活生くん
SPIや玉手箱、その他のWebテストをいろんな企業の選考で受けないといけないのですが、SPI対策以外にもESや面接などに時間を使いたいです。
短期間で合格ラインまで持っていけるような対策法はないのでしょうか？
短期間でSPIやWebテストの対策をして選考にサクッと通過できるようにしたい就活生は多いです。
そこでここでは、短期間でできるSPIやその他のWebテスト選考を通過するための対策法を紹介しますね。
先に結論を伝えておくと、SPIやWebテストの良く出る問題を練習しておくのが一番おすすめですね！
就活アドバイザー 京香
- 対策法：SPIやWebテストのよく出る問題を練習しておく
- 対策法：性格テストの模擬練習をしておく
- 対策法：SPI対策本を買って苦手分野の問題に取り組む
それでは、それぞれ解説していきます。
就活アドバイザー 京香
対策法：SPIやWebテストのよく出る問題を練習しておく
短期間でできるSPIやその他のWebテスト選考を通過するための対策法は「SPIやWebテストのよく出る問題を練習しておく」ことです。
SPIや玉手箱、Webテストでは、毎回似たような問題が数多く出題されるため、頻出問題だけでも勉強しておくことで合格ラインを越えられることが多いです。
そこで問題をたくさん練習したい方は、SPIやWebテストの問題を網羅した「SPI頻出問題集」を使うのがおすすめです。
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
\ 140,000人以上が利用中！ /
SPIの練習問題を解く
（SPI頻出問題集）
＊公式LINE限定で無料配布中！
SPI頻出問題集は「実際の問題と類似してる点が多く、非常に役立ちました。」という非常に信頼性の高い口コミがありますよ。
就活アドバイザー 京香
対策法：性格テストの模擬練習をしておく
短期間でできるSPIやその他のWebテスト選考を通過するための対策法は「性格テストの模擬練習をしておく」ことです。
実は就活生にはあまり知られていないですが、SPIやWebテストでは性格検査で落ちることがよくあります。
言語や非言語の問題だけを対策していると、性格テストで落ちることになってしまうため、性格テストの対策もする必要があります。
そこでおすすめなのが、本番同様にSPIの性格テストを体験できる「適性診断AnalyzeU+」です。
- 251問の質問があるのでSPIやWebテストの性格検査の対策に向いている
- 100万人のデータから診断してくれるのでかなり正確な結果がわかる
- ついでに診断結果からあなたにおすすめの職種もわかる
\ 大手,優良企業からスカウトが届く! /
客観的な性格診断を受ける
（適性診断AnalyzeU+）
＊プロフィール登録で優良企業のスカウトGET！
適性診断AnalyzeU+は「SPIの性格検査以外にもちゃんと自分の強みがわかる」という点で非常に就活生からの評価が高い診断ですよ。
就活アドバイザー 京香
対策法：SPI対策本を買って苦手分野の問題に取り組む
短期間でできるSPIやその他のWebテスト選考を通過するための対策法は「SPI対策本を買って苦手分野の問題に取り組む」ことです。
SPIの対策本には、どのように対策すべきかやどんな問題が出題されるのかが詳しくまとめられています。
そのため、しっかりと対策したい方にはSPIの参考書をおすすめします。
SPIの問題集を反復して解くうちに、SPIの問題形式になれることが出来ます。
解く時にはしっかりと時間を計測して練習しましょうね。
就活アドバイザー 京香
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
SPI推論が苦手な人におすすめの対策法,問題集,アプリ
就活生くん
SPI推論のおすすめの対策法を教えてください！
分かりました。
では、SPI推論のおすすめの対策法を2つ紹介していきます！
「就活の教科書」編集部 平井
- 対策法①：SPIの問題集を解く
- 対策法②：SPIのアプリを使う
SPIの問題集を解く（『史上最強SPI＆テストセンター超実践問題集』など）
SPI推論が苦手な人におすすめの対策法1つ目は、「SPIの問題集を解く」です。
SPI推論を対策する上でもっとも大切なのは、問題に慣れることです。
問題に慣れることで、解き方のパターンも覚えられ、解くスピードも速くなります。
そして推論の問題に慣れるには問題集を繰り返し解くことが効果的です。
1冊の問題を繰り返し解くと、問題パターンごとの解き方を効率よく身に付けられるので、おすすめです。
SPIのおすすめ問題集はこちらの記事で紹介しています！
「就活の教科書」編集部 平井
SPIのアプリを使う（『SPI言語・非言語一問一答』など）
SPI推論が苦手な人におすすめの対策法2つ目は、「SPIのアプリを使う」です。
SPIの問題に慣れるためには、問題集に加えてSPIの対策アプリを使うこともおすすめです。
「SPI言語・非言語 一問一答」が、一番評価の高いアプリケーションになっています。
アプリがあれば、スキマ時間でSPIの対策ができます。
アプリを活用して、たくさんの問題に触れておきましょう。
また、SPI非言語には推論以外にも様々な問題があります。
SPI非言語の他の問題については以下の記事で詳しく解説しているので、ぜひ読んでみてください。
「就活の教科書」編集部 平井
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
まとめ：SPI推論は難問のため、対策が必須
本記事はいかがだったでしょうか？
就活生の皆さんの悩みに少しでも答えられていたら幸いです。
本記事では、「SPIの推論」について徹底解説しました。
併せて、「SPI推論の問題例と解き方」や、「SPI推論は捨てるべきか？」についても紹介しました。
最後にこの記事を簡単にまとめておきます。
◆【特徴を解説】SPIの推論とは
- SPI推論の問題の特徴
- SPI推論の出題頻度
- SPI推論は難しい
◆SPI推論の問題例と解き方
- SPI推論の問題例①：順序
- SPI推論の問題例②：密度
- SPI推論の問題例③：発言の正誤
- SPI推論の問題例④：対戦
- SPI推論の問題例⑤：位置
- SPI推論の問題例⑥：平均
- SPI推論の問題例⑦：内訳
◆SPI推論の解き方のコツや対策方法
- SPI推論の解き方のコツ①：問題をしっかり読む
- SPI推論の解き方のコツ②：図式化して整理する
- SPI推論の解き方のコツ③：設問内容から確実に言えることだけで判断する
- SPI推論の解き方のコツ④：解き方を覚える
- SPI推論の解き方のコツ⑤：過去問や問題集を使って問題に慣れる
◆SPI推論は捨てるべき？
- 結論：推論は捨てるべきでない
- 理由：推論はSPIで高得点を取るためには必須だから
◆SPI推論が苦手な人におすすめの対策法
- SPIの問題集を解く
- SPIのアプリを使う
◆まとめ：SPI推論は難問のため、対策が必須