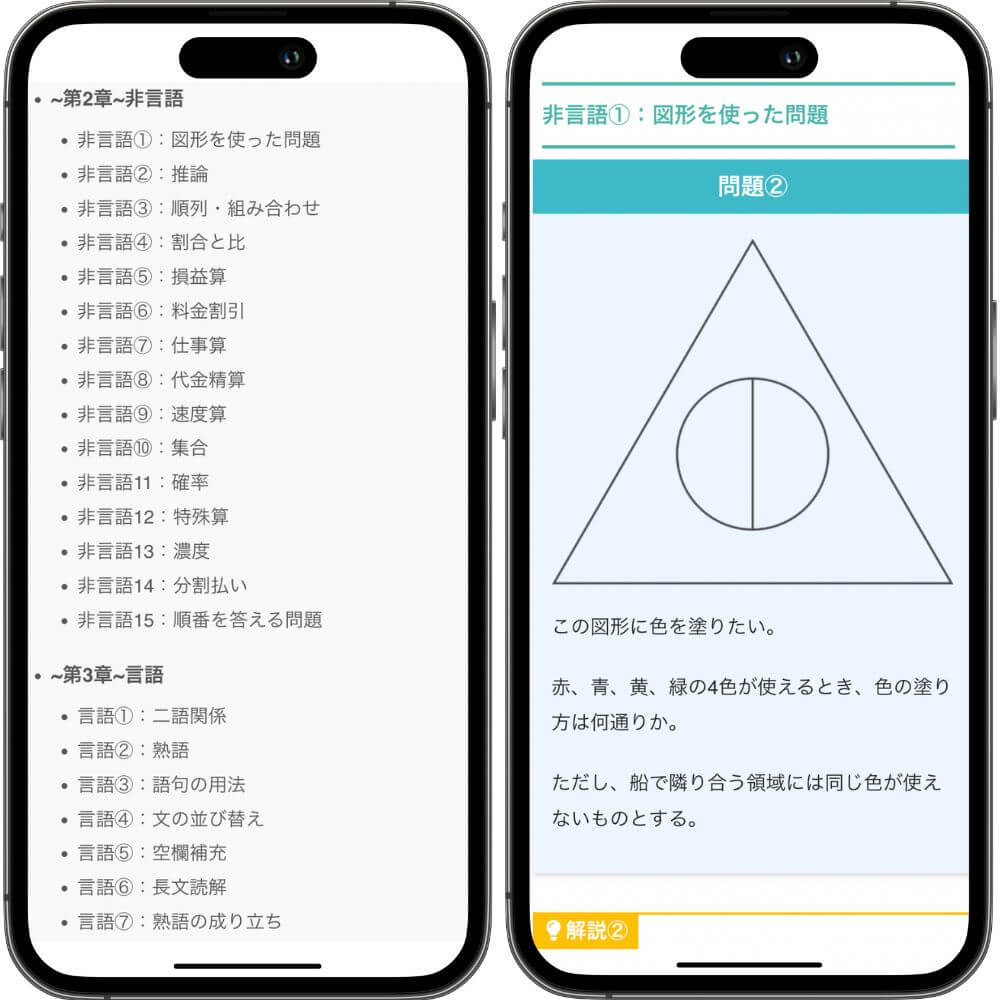
- 組み合わせ：〇個の異なるものの中から△個を選ぶときのパターンのこと
- 組み合わせの練習問題と解説
- 組み合わせのおすすめ勉強法
- 組み合わせに関するよくある質問
-
Webテスト（SPI,玉手箱など）の対策には、以下のツールがおすすめ
-
【就活生/転職者】SPI頻出問題集（LINEで無料配布）
（SPI/Webテストの頻出問題を練習） -
【就活生】Lognavi WEBテスト
（言語・非言語118問,性格診断90問） -
【就活生】適性診断AnalyzeU+
（251問で性格診断）
-
【就活生/転職者】SPI頻出問題集（LINEで無料配布）
この記事では、組み合わせの公式や解き方のコツについて解説します。
また、組み合わせのおすすめの対策法や練習問題なども紹介しています。
ちなみに、「SPIやテストセンターで落ちたくない」「Webテストを効率的に勉強したい」という人は、SPIやWebテストの例題を短時間で練習できる「SPI頻出問題集（公式LINEで無料配布）」などのサービスを活用しましょう。
この記事を読めば「組み合わせの問題の解き方がわからない」「WEBテストの組み合わせ問題の例題や解説が欲しい」などの不安はなくなります。
- 組み合わせの解き方が知りたい
- 組み合わせと順列の違いを理解したい
- 組み合わせ問題を実際に解いて練習したい
- 組み合わせの勉強法を知りたい
上記に当てはまる就活生は、ぜひこの記事を読んでみてください。
「SPIなどのWebテストで落とされたくない！」という方には「SPI頻出問題集」で本番の問題に近い練習をして、効率良く得点をUPさせるのがおすすめです。
ちなみに「SPI頻出問題集」以外にも、SPI模擬テストが受けられる「Lognavi WEBテスト」、251問の性格診断「適性診断AnalyzeU+」もおすすめですよ。
就活アドバイザー 京香
- 【就活生/転職者】SPI頻出問題集（公式LINEで無料配布）
【公式サイト】https://reashu.com/linelp-spi/
- Webテストで頻出の問題がわかる
- 【就活生】Lognavi WEBテスト（言語・非言語118問,性格90問）
【公式サイト】https://lognavi.com/
- 自分の実力を客観的に知れる
- 【就活生】適性診断AnalyzeU+（全251問、客観的な性格診断）
【公式サイト】https://offerbox.jp/
- 診断でSPI性格検査の練習も
「結局どのサービスを使えば良いかわからない…」という方は「SPI頻出問題集」で練習問題を解いてみるのが一番おすすめですよ。
就活アドバイザー 京香
目次
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
【SPIで出る！】そもそも組み合わせとは？
就活生ちゃん
SPIの対策をしたいのですが、そもそも組み合わせの解き方がわかりません。
就活生くん
僕は順列と組み合わせの違いについて教えてほしいです。
組み合わせについてよく知らない方もいますよね。
ではまず、組み合わせについてざっくり説明します。
就活アドバイザー 京香
組み合わせ：〇個の異なるものの中から△個を選ぶときのパターンのこと
組み合わせとは、「〇個の異なるものの中から△個を選ぶときのパターンのこと」を指します。
例えば、4個の異なる文字から3個を選ぶ、というのも組み合わせの問題の1つです。
A, B, C, Dのアルファベット4文字から3文字を選ぶ場合、組み合わせは、（A, B, C）（A, B, D）（A, C, D）（B, C ,D）の4通りとなります。
問題文から組み合わせの問題であると気づくことも大切です！
「〜◯個選ぶときの〜」「〜ずつ分けるときの〜」といったフレーズに注意しましょう。
就活アドバイザー 京香
組み合わせと順列の違い
組み合わせと順列の違いは、「順序を考慮するかしないか」の違いです。
順列は「◯個の異なるのものの中から△個取り出して並べるときのパターンのこと」を指します。
順列の場合、並び順の前後が入れ替わっていれば、全く別のものとして捉えます。
例えば、（A, B, C）と（A, C, B）は、使われているアルファベットは同じですが、順番が異なっているので別物となります。
一方で、組み合わせの場合、順番が違っていても最終的に取り出した△個が同じ種類であれば、同一のものとみなします。
例えば、（A, B, C）と（A, C, B）は順番が違っても選ばれた3つのアルファベットが同じ種類であるため、同じものとして扱われます。
この違いを押さえておくことで、計算方法のミスを防ぐことができるので、しっかり覚えておきましょう！
就活アドバイザー 京香
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
【解き方も解説】組み合わせの公式と例題7選
就活生くん
組み合わせと順列の違いについては分かったのですが、簡単に求めるための公式があれば教えてほしいです。
それでは、組み合わせの公式を紹介します。
就活アドバイザー 京香
組み合わせの公式と解説
組み合わせの問題を解くときには、nCrという公式を用います。
nには異なるものの総数、rには選ぶ数を当てはめます。
この公式を用いた計算は、分子でn×(n-1)×(n-2)×・・・×{n-(n-1)}×1、分母でr×(r-1)×(r-2)×・・・×{r-(r-1)}×1をします。
4個の異なるものから3個を選ぶ組み合わせを求める場合、nCrの公式を利用して計算すると、（4×3×2×1）/（3×2×1）＝4となり、4通りを導くことができます。
組み合わせの式で使われるCは組み合わせを意味する英単語「combination（コンビネーション）」の頭文字から取られています。
就活生ちゃん
組み合わせの公式を覚えたので、問題を解く練習をしたいです。
それでは、組み合わせの例題と解説を7つ紹介します。
就活アドバイザー 京香
- 例題①：決まった2組に分ける組み合わせ
- 例題②：ランダムな2組に分ける組み合わせ
- 例題③：決まった3組に分ける組み合わせ
- 例題④：ランダムな3組に分ける組み合わせ
- 例題⑤：不均等に分ける組み合わせ
- 例題⑥：重複組み合わせ
- 例題⑦：順列と組み合わせの複合問題
例題①：決まった2組に分ける組み合わせ
例題1つ目は、「決まった2組に分ける組み合わせ」です。
Aさん, Bさん, Cさん, Dさん, Eさん, Fさんの6人を3人ずつ、赤組と白組の2組に分けると何通りに分けられるでしょうか。
【解答】
20通り
【解説】
この問題では「3人ずつ分ける」と何通りになるか聞かれているので、組み合わせの問題だとわかります。
赤組の3人が決まれば、白組の3人も決まるので、赤組になる3人の組み合わせが何通りかを求めれば、答えを導くことができます。
計算の仕方は以下のとおりです。
6C3＝（6×5×4）/（3×2×1）＝20
したがって、答えは20通りとなります。
例題②：ランダムな2組に分ける組み合わせ
例題2つ目は「ランダムな2組に分ける組み合わせ」です。
Aさん, Bさん, Cさん, Dさん, Eさん, Fさんの6人を3人ずつの2組に分けると何通りに分けられるでしょうか。
【解答】
10通り
【解説】
例題②と例題①の違いは、分ける2つの組に区別がされていない点です。
2つの組に区別があれば、
（赤組：A, B, C / 白組：D, E, F）
（赤組：D, E, F / 白組：A, B, C）
の2つが別物として区別できますが、今回の問題には組の区別がないため、上記の2組は同じ1通りのものとみなされます。
以上のことを踏まえると、計算の仕方は以下のとおりです。
6C3/2＝（6×5×4）/（3×2×1）×1/2＝10
したがって、答えは10通りとなります。
例題③：決まった3組に分ける組み合わせ
例題3つ目は「決まった3組に分ける組み合わせ」です。
Aさん, Bさん, Cさん, Dさん, Eさん, Fさんの6人を3人ずつ、赤組・白組・青組の3組に分けると何通りに分けられるでしょうか。
【解答】
90通り
【解説】
赤組の2人、白組の2人を選べば、残りの2人が青組に決まるので、赤組2人と白組2人の組み合わせが何通りかを求めれば、答えを導くことができます。
以上のことを踏まえると、計算の仕方は以下のとおりです。
6C2×4C2＝（6×5）/（2×1）×（4×3）/（2×1）＝90
したがって、答えは90通りとなります。
練習問題④：ランダムな3組に分ける組み合わせ
例題4つ目は「ランダムな3組に分ける組み合わせ」です。
Aさん, Bさん, Cさん, Dさん, Eさん, Fさんの6人を3人ずつ3組に分けると何通りに分けられるでしょうか。
【解答】
15通り
【解説】
例題④と例題③は、例題②と例題①の違いと同様に、組の区別がない点です。
3つの組に区別がない場合、
（赤組：A, B / 白組：C, D / 青組：E, F）
（赤組：A, B / 白組：E, F / 青組：C, D）
（赤組：C, D / 白組：E, F / 青組：A, B）
（赤組：C, D / 白組：A, B / 青組：E, F）
（赤組：E, F / 白組：A, B / 青組：C, D）
（赤組：E, F / 白組：C, D / 青組：A, B）
の6通りが全て同じ1通りの分け方とみなされます。
以上のことを踏まえると、計算の仕方は以下のとおりです。
6C2×4C2/6＝（6×5）/（2×1）×（4×3）/（2×1）×1/2＝15
したがって、答えは15通りとなります。
「区別されない◯組に分ける」問題の場合、nCrで求めた値を◯!で割ることで答えを求めることができます。
例題④の場合は、6C2×4C2/3!となります。
就活アドバイザー 京香
例題⑤：不均等に分ける組み合わせ
例題5つ目は「不均等に分ける組み合わせ」です。
Aさん, Bさん, Cさん, Dさん, Eさん, Fさんの6人を、赤組3人・白組2人・青組1人の3組に分けると何通りに分けられるでしょうか。
【解答】
60通り
【解説】
赤組の3人、白組の2人を選べば、残りの1人が青組に決まるので、赤組3人と白組2人の組み合わせが何通りかを求めれば、答えを導くことができます。
以上のことを踏まえると、計算の仕方は以下のとおりです。
6C3×3C2＝（6×5×4）/（3×2×1）×（3×2）/（2×1）＝60
したがって、答えは60通りとなります。
例題⑥：重複組み合わせ
例題6つ目は「重複組み合わせ」です。
赤、青、黄から重複を許して3つを選ぶ方法は何通りあるでしょうか。
【解答】
10通り
【解説】
まず、「重複を許す」という表現の意味を説明します。
これまでの例題では、1度用いられた要素を2度使うことはできませんでした。
しかし、今回の問題では、一度用いられた要素を複数回使うことができます。
例題⑥の場合、（赤、青、黄）（赤、赤、黄）（赤、赤、赤）といった組み合わせが可能になります。
重複組み合わせの問題を解くときは、樹形図を描くと視覚的に理解ができるので、考えやすいです。
または、以下の考え方を利用して解くこともできます。
重複組み合わせの際には、どのタイミングで要素が変わるのかが重要です。
要素が変わるタイミングを｜で示すと、それぞれの要素
（赤、青、黄）（赤、赤、黄）（赤、赤、赤）は、
赤｜青｜黄、赤赤｜黄｜、赤赤赤｜｜と表すことができ、
求める組み合わせは、3つの要素と2つの｜の5つの並べ方と考えることができます。
よって、以上より5C3＝（5×4×3）/（3×2×1）＝10通りとなります。
したがって、答えは10通りです。
例題⑦：順列と組み合わせの複合問題
例題7つ目は「順列と組み合わせの複合問題」です。
SPIでは以下のように順列と組み合わせを掛け合わせた、少々複雑な問題が出題されることがあります。
赤、青、黄の3色のボールから2つを選び、選んだ2つのボールを並べる方法は何通りあるでしょうか。
【解答】
6通り
【解説】
この問題は、3色のボールから2つを選ぶ「組み合わせ」と、選ばれた2つのボールの並び方を求める「順列」の複合問題だとわかります。
まず、3色のボールから2つを選ぶ組み合わせを求めます。
組み合わせの公式を利用して、3C2＝（3×2）/（2×1）＝3通りとなります。
ここで、2つのボールの並べ方を求めると、
2P2＝2×1＝2通りが求められます。
3通りの組み合わせそれぞれに2通りの並べ方があるので、求める結果は
3×2＝6
したがって、答えは6通りです。
参照：組み合わせとは？誰でも理解できるようにわかりやすく解説 | HEADBOOST、SPI 『順列・組合せ（場合の数）』 ～練習問題と解き方を徹底解説！～ ｜ SPI練習問題(数学徹底解説)-非言語対策
公式を利用して素早く答えを求められる問題から、発想力が試される問題まで様々な種類の問題がありますね。
繰り返し練習して、解き方を理解しましょう！
就活アドバイザー 京香
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
組み合わせのおすすめ勉強法
就活生くん
組み合わせの問題をもっと練習して、WEBテストに備えたいです。
おすすめの勉強法を教えてもらえませんか？
わかりました。
組み合わせのおすすめ勉強法を3つ紹介します。
就活アドバイザー 京香
- 勉強法①：問題集を繰り返し解き、解き方のパターンを覚える
- 勉強法②：ただ暗記をするのではなく、考え方を理解しておく
- 勉強法③：問題に慣れてきたら、時間配分も意識して解いてみる
その①：問題集を繰り返し解き、解き方のパターンを覚える
組み合わせのおすすめ勉強法1つ目は「問題集を繰り返し解き、解き方のパターンを覚える」です。
この問題集では、SPIでよく出題される組み合わせの問題の練習をすることができます。
多くの就活生が活用していて、計数問題の解説も丁寧にされているので、おすすめの教材です。
ぜひ利用してみてください。
練習を繰り返し行い、組み合わせの解き方を身につけましょう！
就活アドバイザー 京香
その②：ただ暗記をするのではなく、考え方を理解しておく
組み合わせのおすすめ勉強法2つ目は「ただ暗記をするのではなく、考え方を理解しておく」です。
この記事で組み合わせの公式について紹介しましたが、重要なのは公式ではなく問題の考え方です。
考え方を理解していれば、万が一公式を忘れてしまっても、答えを求めることができます。
問題を解くときには、公式と答えだけではなく解説まで確認して、解き方を理解しましょう！
就活アドバイザー 京香
その③：問題に慣れてきたら、時間配分も意識して解いてみる
組み合わせのおすすめ勉強法3つ目は「問題に慣れてきたら、時間配分も意識して解いてみる」です。
就活のWEBテストには時間制限があり、一つの問題に時間をかけ過ぎてしまうことで他の問題に手が回らず、選考に落ちてしまうこともあります。
問題に慣れるまでは時間をかけてじっくり理解し、慣れてきたらストップウォッチで時間を計りながら、素早く解けるように練習してみましょう！
より実践的に練習することを意識しましょう！
就活アドバイザー 京香
SPI/テストセンターの対策に役立つ記事一覧
「志望企業の選考にSPIがあるけど、時間が足りない」という就活生には以下の記事がおすすめです。
以下の記事を読めば、SPIの能力検査と性格検査対策方法について知れ、簡単に選考を通過できるようになるので、ぜひ参考にしてください。
就活アドバイザー 京香
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
組み合わせに関するよくある質問
就活生ちゃん
だんだん組み合わせについてよくわかってきました！
他に組み合わせに関して、何か知っておいた方が良いことはありますか？
それでは最後に、組み合わせに関するよくある質問について2つご紹介します！
就活アドバイザー 京香
- 質問①：組み合わせ問題が苦手な人の特徴は？
- 質問②：組み合わせの公式の証明を教えて！
質問①：組み合わせ問題が苦手な人の特徴は？
組み合わせに関するよくある質問1つ目は「組み合わせ問題が苦手な人の特徴は？」です。
結論からいうと、組み合わせ問題が苦手な人は、発想力に自信がないということが考えられます。
組み合わせは、数学的な思考力に加え、発想力も必要になります。
ですが、発想力に自信がなくても問題を解く練習を重ねれば苦手意識を減らすことができます。
WEBテストの勉強不足が原因で納得のいく就活ができなかった・・・と後悔することがないようにしましょう！
就活アドバイザー 京香
質問②：組み合わせの公式の証明を教えて！
組み合わせに関するよくある質問2つ目は「組み合わせの公式の証明を教えて！」です。
以下に組み合わせの公式の証明を紹介します。
結論から言うと、組み合わせの公式は、単純に「順列を、1 組の組み合わせの中に含まれている順列の数（同じ組み合わせで並び方が異なるものの重複数）で割る」ということをしているだけです。
例としてA, B, C, Dの4つの要素から3つを取り出して並べる場合（順列の場合）と、取り出すだけの場合（組み合わせの場合）を考えてみましょう。このとき順列は以下の24通りあります。
- {ABC, ACB, BAC, BCA, CAB, CBA}
- {ABD, ADB, BAD, BDA, DAB, DBA}
- {ACD, ADB, CAD, CDA, DAC, DCA}
- {BCD, BDC, CBD, CDB, DBC, DCB}
このように見てみると、1行目の6つの順列はすべて同じABCの組み合わせでできていることがわかります。同じように2行目の6つの順列はABDの、3行目の6つの順列はACDの、4行目の6つの順列はBCDの組み合わせであることがわかります。
つまり1組の組み合わせの中に6つの順列が含まれているのです（言い方を変えると、同じ組み合わせで並び方が異なるものが、それぞれのパターンで6つずつある）。以上のことから、この場合の組み合わせの数は、順列を6で割ることで求められることがわかります。
4C3=4P3/6=24/6=4さて、分母の6は「1組の組み合わせの中に含まれている順列の数（同じ組み合わせで並び方が異なるものの重複数）」ですが、これは一々書き出さなくても簡単に求めることができます。
たとえばn個の要素から2つを取り出す場合の組み合わせであれば、重複数は必ず 2P2=2!になります。n個の要素から3つを取り出す場合の組み合わせであれば、重複数は必ず 3P3=3!になります。つまり公式から組み合わせを求める際の分母は rPr=r!で求められるのです。
なぜなら、いかなるn個の要素からだとしても、取り出すのはr個だからです。そしてr個の順列rPrは、必ず重複数と同じになるのです。
さて、ここまでを式でまとめると次のようになります。
nCr＝nPr/rPr＝nPr/r!
これが組み合わせの公式の証明です。
引用：組み合わせとは？誰でも理解できるようにわかりやすく解説 | HEADBOOST
順列で求めたもののうち、同じ要素で構成されたものを省くというのが基本的な考え方のようですね！
就活アドバイザー 京香
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
まとめ：組み合わせの公式を定着させて、Webテストを確実に突破しよう！
今回は、組み合わせについて解説しました。
あわせて、組み合わせの例題・解説や、組み合わせの勉強法などを紹介しました。
組み合わせはWEBテストで頻出なので、必ず対策が必要です。
数学が苦手な人は、記事で紹介したSPIの問題集を使い、組み合わせの練習をしましょう。
この記事を読んだことで、組み合わせやWEBテストに関する不安や疑問が解消されていたら、嬉しい限りです。