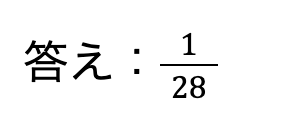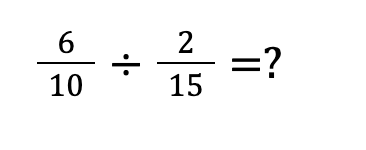- 分数の足し・引き・かけ算・割り算のやり方
- 分数から少数へ転換する方法
- SPIを突破するためのおすすめの勉強方法
- 分数を計算するときのコツ
-
Webテストの対策には、以下のツールがおすすめ
-
【就活生】SPI頻出問題集（LINEで無料配布）
（SPI/Webテストの問題練習） -
【就活生】Lognavi適性診断
（性格テスト90問、SPI練習問題） -
【就活生】適性診断AnalyzeU+
（251問で性格診断、人気No.1）
-
【就活生】SPI頻出問題集（LINEで無料配布）
この記事では、「分数の計算方法」について詳しく解説していきます。
あわせて、
- 「分数から少数に直す方法」
- 「SPIを突破するための勉強方法」
- 「分数を計算するコツ」
についても解説します。
「SPIのテストを突破できるか不安…」という不安が解消されるので、ぜひ最後まで読んでみてください。
「SPIなどのWebテストで落とされたくない！」という方には「SPI頻出問題集」で実際の問題に近い演習をし、短期間で得点をUPさせるのがおすすめです。
ちなみに「SPI頻出問題集」以外にも、SPI練習問題110問、性格テスト90問ができる「Lognavi適性診断」、251問で性格診断、人気No.1の「適性診断AnalyzeU+」もおすすめですよ。
就活アドバイザー 京香
- 【就活生/転職者】SPI頻出問題集（公式LINEで無料配布）
【公式サイト】https://reashu.com/linelp-spi/
- Webテストで頻出の問題がわかる
- 【就活生】Lognavi（SPI問題が208問：知的118問,性格90問）
【公式サイト】https://lognavi.com/
- テスト結果から最適企業を表示
- 【就活生】適性診断AnalyzeU+（全251問、人気No.1の性格診断）
【公式サイト】https://offerbox.jp/
- 診断でSPI性格検査の練習も
「結局どのサービスを使えば良いかわからない…」という方は「SPI頻出問題集」で練習問題を解いてみるのが一番おすすめですよ。
就活アドバイザー 京香
目次
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
【SPI対策】分数の計算方法を復習しておこう！
就活生ちゃん
いつもSPIで分数の計算方法が分からず、勘で答えてしまっています…
分数の計算方法を教えてください。
では、まず分数の計算方法を復習しましょう！
その後、SPIで出題される分数問題の特徴も解説します。
最後まで読んで、分数問題を素早く解けるよう練習しましょう！
就活アドバイザー 京香
分数の計算のやり方
分数の計算方法は「足し算・引き算」「かけ算」「割り算」で異なります。
以下にそれぞれの場合の計算方法を簡単に記載しているので、参考にしてください。
ですが、分数の計算には1つ共通点があります。
それは、分数の計算では、必ず約分をすることです。
約分をしないと間違っていることになるため、必ず約分をしましょう。
約分とは、分母と分子を同じ数で割って分数の値を単純化することです。
例えば、2/4という分数がある時、分子と分母の両方を2で割って1/2の形にすることを約分と言います。
SPIは記述ではなく選択肢形式ですが、分数は必ず約分して単純化された数字が選択肢にあります。
自身で計算して答えを出したけれど選択肢に答えと同じ数字がない場合、約分が出来そうか考えてみましょう。
以下に、各場合の計算方法を例題付きで解説しています。
詳しいやり方を知りたい人は、知りたい計算方法をタップすると該当部分にとべますよ！
就活アドバイザー 京香
SPIで出題される分数問題の特徴
SPIで出題される分数問題の特徴として、文章を読んで計算することが挙げられます。
SPIは計算式が既に与えられており、それに基づいて計算するのではありません。
文章を読んで、そこからどの数字を使ってどうやって計算すれば良いか考える必要があります。
出題頻度の高い問題としては、確率、割合と比、料金の割引などがあります。
以下に例題を記載を記載するので、ぜひチャレンジしてみてください！
就活アドバイザー 京香
ある中学校で、全校生徒の50％がA小学校出身で、その数は300人である。
この時、全校生徒の20％を占めるB小学校出身者は何人か。
答え：120人
＜解説＞
B小学校出身者の人数を知るためには、全校生徒の数を知る必要があります。
全校生徒の数は「A小学校出身者は300人で、全校生徒の50％を占める」ことを使えば導けます。
全校生徒の数×50%(50/100)=300人より、
300÷50/100=600 ⇒全校生徒は600人
求めるB小学校出身者は全校生徒の20％を占めるため、
600×20/100=120 ⇒B小学校出身者は120人
問題ごとに解き方のパターンがあるので、何度も練習して慣れていきましょう！
就活の教科書では「SPI頻出問題集」をプレゼントしています。
SPIに自信がない人はこの機会にゲットして対策を進めましょう！
就活アドバイザー 京香
「SPIやWebテストの対策どうしよう…」「正直、短時間で点数を上げたい！」という方は、公式LINEで無料配布しているSPI頻出問題集を使うのがおすすめですよ。
SPI頻出問題集では、非言語と言語の頻出問題だけを網羅しているので、練習すれば短期間でボーダーを超えられますよ。
SPIやWebテストの対策を早く終わらせたい方は、ぜひ利用してみてくださいね。
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
（SPI頻出問題集）
【例題あり】分数の練習問題と解説
就活生ちゃん
足し算・引き算・かけ算・割り算別の計算方法が分からず、いつも時間内に問題が解けません…
具体的な計算方法を例題付きで教えて欲しいです。
では、ここから例題を使いながら、詳しい分数の計算方法を解説していきます。
分数の計算に自信がない人は最後まで見て、練習を繰り返して慣れていきましょう！
就活アドバイザー 京香
例題①：分数の足し算
まず足し算では、分母の数を同じにする必要があります。
分母の数を同じにすることを「通分」と言います。
通分をした後、分子同士の足し算をして、最後に可能であれば約分をします。
下の例題を使って計算してみましょう！
就活アドバイザー 京香
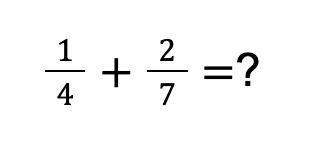
STEP①：通分をする
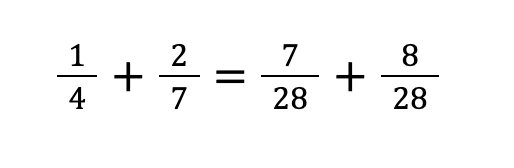
通分をする時、分母の数を大きくしただけ分子の数も大きくする必要があります。
1/4の場合、分母に7を掛けているため、分子にも7をかける必要があります。
通分をする時は、片方の分母の数をかけると素早くできます！
例えば、分母が5と6の場合、5には6をかけて、6には5をかけると分母を揃えることが出来ます。
就活アドバイザー 京香
STEP②：分子の足し算をする
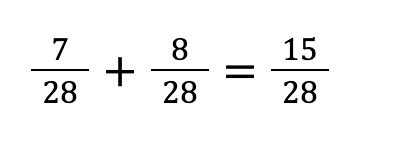
STEP③：約分をする
今回は約分できないため、15/28で正解となります。
例題②：分数の引き算
引き算では足し算と同様に、分母の数を同じにする（通分）必要があります。
通分をした後、分子の引き算をして、最後に可能であれば約分をします。
下の例題を使って計算してみましょう！
就活アドバイザー 京香
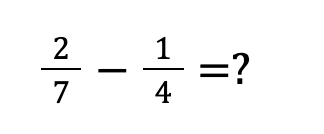
STEP①：通分をする
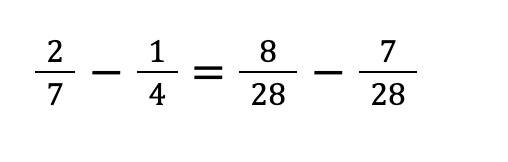
通分をする時、分母の数を大きくしただけ分子の数も大きくする必要があります。
1/4の場合、分母に7を掛けているため、分子にも7をかける必要があります。
通分をする時は、分母同士をかけると素早くできます！
就活アドバイザー 京香
STEP②：分子の引き算をする
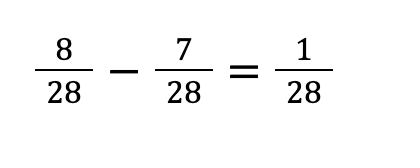
STEP③：約分をする
今回は約分できないため、1/28で正解となります。
例題③：分数の掛け算
分数の掛け算では、分母同士・分子同士で掛け算をします。
掛け算でも約分をしますが、掛け算を行う前に約分を行うと計算が楽になります。
下の例題を使って計算してみましょう！
就活アドバイザー 京香
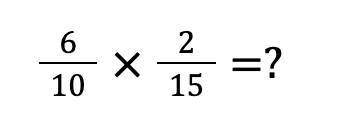
STEP①：約分をする
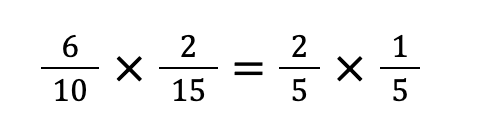
分数の掛け算で約分を行う時、1つの分数の分母（分子）と、片方の分子（分母）で約分を行うと計算が楽になります。
今回の場合、左側の分数の分母である「10」と、右側の分数の分子である「2」で約分ができます。
また、左側の分数の分子である「6」と、右側の分数の分母である「15」でも約分ができ、計算が楽になります。
分母同士・分子同士での約分は出来ないので気をつけましょう！
就活アドバイザー 京香
STEP②：掛け算をする
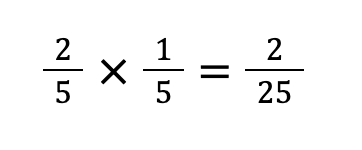
例題④：分数の割り算
分数の割り算では、右側の分数の分母と分子を反対にして掛け算にして計算します。
割り算でも答えを約分する必要がありますが、掛け算に直した後に約分をすると計算が楽になります。
下の例題を使って計算してみましょう！
就活アドバイザー 京香
STEP①：右側を反対にする
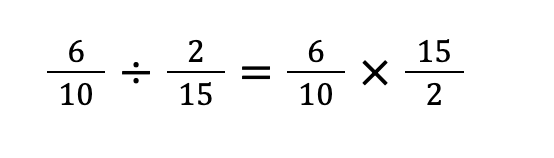
割り算は正式には「割られる数÷割る数」という構造になっています。
分数の割り算では、割る数の分母と分子を反対にして、掛け算として計算することで計算できます。
STEP②：約分をする
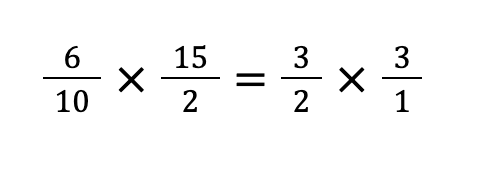
分数の掛け算で約分を行う時、1つの分数の分母（分子）と、片方の分子（分母）で約分を行うと計算が楽になります。
今回の場合、左側の分数の分母である「10」と、右側の分数の分子である「15」で約分ができます。
また、左側の分数の分子である「6」と、右側の分数の分母である「2」でも約分ができ、計算が楽になります。
分母同士・分子同士での約分は出来ないので気をつけましょう！
就活アドバイザー 京香
STEP③：計算する
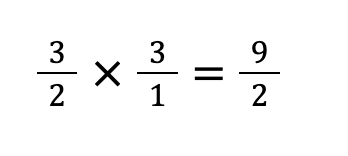
例題⑤：分数から少数への変換
分数から少数へ変換するには、「分子÷分母」を計算するだけで出来ます。
SPIの中には分数を少数に変換して答える問題もあるため、練習して慣れておきましょう。
以下に例題を複数用意しているので、解答を見る前に計算してみましょう！
就活アドバイザー 京香
1÷2=0.5
2÷5=0.4
4÷25=0.16
A.0.25
%は分数で表すことができ、「％の数字/100」という形になります。
25％であれば25/100、つまり25÷100=0.25となります。
分数から少数に変換する時、例題のような割り切れる分数だけでなく、割り切れない分数もあります。
例えば、1/3=0.333333…のように、答えが終わらないものもあります。
ですが、SPIの問題では必ず四捨五入をして答えるようになっているので、割り切れない場合でも問題はありません。
例題⑥：分数比から整数比への変換
分数比から整数比に変換するには、分数に公倍数を掛けて分母を消去することで出来ます。
公倍数とは、2つ以上の整数に共通する倍数のことです。
例えば、3と5の公倍数は、15・30・45などがあります。
分数比を整数比へ変換するには、2つの分数に公倍数をかけて分母を消去する必要があります。
以下に例題を用意しています。
答えと解説を見る前に、ぜひ自分で計算してみてください！
就活アドバイザー 京香
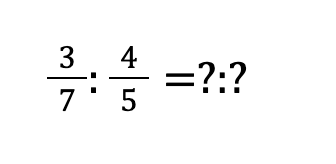
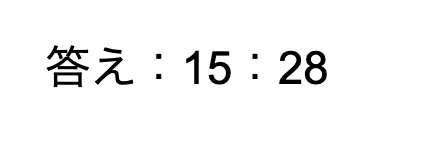
STEP①：2つの分数の分母の公倍数を探す
今回は分母が7と5であるため、公倍数は35です。
公倍数を探す時は、数が小さい場合は分母を掛け算した数字（5×7＝35）で計算すると良いでしょう。
数が大きい場合は少し変わったテクニックを使うと簡単に公倍数が求められます。
以下に記載するので、興味のある方はぜひ参考にしてください。
大きい数の公倍数の探し方は、
①：16と24を一緒に割り切れるまで割り算していく
②：割った数と最後の余った数を全て掛け算する
この2つの手順で行います。
例えば、16と24の公倍数を探すとします。
①：16と24を一緒に割り切れるまで割り算していく
16と24を一緒に割れる数字を探すと、まずは「2」で割れそうです。
16と24をそれぞれ2で割ると、16÷2=8, 24÷2=12となります。
その後、8と12も同じように割り算していきます。
8と12であれば、もう1度「2」で割れるため、8÷2=4, 12÷2=6となります。
これを同時に割り算できる数字がなくなるまで繰り返します。
4と6の場合、もう1度「2」で割って、4÷2=2, 6÷2=3となり、2と3は同時に割れないため、ここで終了です。
②：割った数と最後の余った数を全て掛け算する
今回は「2」で3回割り、最後の余った数字が「2」と「3」になりました。
これらを全て掛けた数字が16と24の公倍数になります。
2×2×2×2×3＝48
STEP②：公倍数を各分数にかける
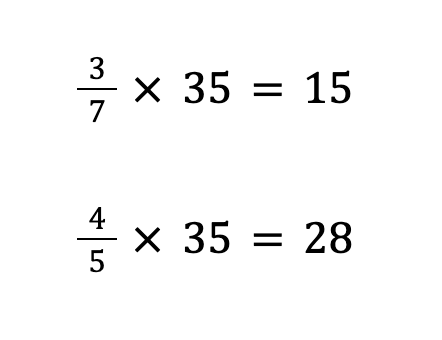
比では、両方に同じ数をかければ比は変わらないです。
なので、3/7と4/5の両方に公倍数を掛けて分母を消すことで答えが出ます！
就活アドバイザー 京香
おまけ：分数を使った割合・確率の計算
分数を使った割合と確率の問題を用意したので、計算方法を復習できたらぜひ挑戦してください！
分数を使った割合と確率は頻出なので、しっかり対策してテスト本番に臨んでくださいね！
就活アドバイザー 京香
割合の問題
答え：5/24
＜解説＞
求める数字の条件は「東京が行き先」かつ「日本人」です。
まず、行き先が海外ではない人の割合は「全体-海外に行く人」であるため、1-1/6=5/6となります。
その中でも、1/3が東京で、東京に行く人の中でも3/4が日本人となるため、これらを全て掛けた数字が答えになります。
5/6×1/3×3/4=5/24
確率の問題
答え：5/18
＜解説＞
片方だけが3の目である確率は以下の2通りの場合が考えられる
- Xが3でYは3以外
- Xが3以外でYは3
Xが3でYは3以外が起こる確率は「1/6×5/6=5/36」となる。
2つ目の場合でも確率は同様であるため、5/36×2=5/18となる。
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
SPIを突破するための分数おすすめ勉強法
就活生ちゃん
分数以外の分野も苦手なのですが、どうやって勉強したら良いですか？
では、以下にSPIを突破するためのおすすめ勉強法を3つ紹介するので、ぜひ参考にしてください！
就活アドバイザー 京香
- その①：問題集を繰り返し解き、解き方のパターンを覚える
- その②：ただ暗記をするのではなく、考え方を理解しておく
- その③：問題に慣れてきたら、時間配分も意識して解いてみる
その①：問題集を繰り返し解き、解き方のパターンを覚える
SPIを突破するための勉強法1つ目は、問題集を繰り返し解き、解き方のパターンを覚えることです。
SPIの問題には傾向があり、問題のタイプごとに解き方があります。
例えば、確率問題で「少なくとも〜〜」という問題の場合、1-事象のおこならい確率で計算することで求まります。
解き方のパターンを覚えることで、短い時間で正確に答えることができ、正答率も上がるでしょう。
以下におすすめの問題集を2つ記載するので、これらを使ってSPI対策を進めましょう。
就活アドバイザー 京香
これが本当のＳＰＩ３だ！ ２０２６年度版 【主要３方式〈テストセンター・ペーパーテスト・ＷＥＢテステ...
おすすめ問題集の1つ目は、「これが本当のSPI3だ！」です。
問題の解説だけでなく、SPIのテスト形式の説明もあるため、これからSPIの対策を始めるという方は特におすすめの問題集です。
この本がおすすめな人を以下に記載するので、ぜひ参考にしてください。
- SPIの形式があまり分からない
- どんな問題が頻出なのか分からない
- 解説が充実している問題集が欲しい
おすすめ問題集の2つ目は、「SPI＆テストセンター超実践問題集」です。
この本は例題と問題が豊富にあり、さらに頻出度順となっているため効率よくSPI対策を進めることができます。
数をこなしてSPIの対策を進めていきたい人には特におすすめの問題集です。
他にもこの本がおすすめな人を以下に記載するので、ぜひ参考にしてください。
- とにかく問題の数をこなしたい
- 少し難易度の高い問題も欲しい
- 解説が充実した問題集が欲しい
その②：ただ暗記をするのではなく、考え方を理解しておく
SPIを突破するための勉強法1つ目は、ただ暗記をするのではなく、考え方を理解しておくことです。
当然ですが、本番のテストで出る問題は、問題集などと異なる数字で出題されます。
そのため、ただ問題文と答えを暗記していては、本番に問題を解ける実力は備わりません。
本番に問題を解けるようになるためにも、「どうやって考えるか」を理解しておきましょう。
上で紹介した問題集は解説の中に「どうやって考えれば良いか」も記載しています！
ぜひ問題集を手に取って、対策を進めていきましょう。
就活アドバイザー 京香
その③：問題に慣れてきたら、時間配分も意識して解いてみる
SPIを突破するための勉強法1つ目は、問題に慣れてきたら、時間配分も意識して解いてみることです。
SPIは短い時間で大量の問題を解く必要があります。
そのため、1問にかける時間には限りがあり、スピード感を持って解いていかないといけません。
本番で時間内に終わらせるには、普段の練習から時間配分も意識して解いてみましょう。
自分はどの問題に時間がかかる傾向にあるか把握しておくと、本番でも時間の使い過ぎを防げるかもしれません！
就活アドバイザー 京香
SPI/テストセンターの対策に役立つ記事一覧
「志望企業の選考にSPIがあるけど、時間が足りない」という就活生には以下の記事がおすすめです。
以下の記事を読めば、SPIの能力検査と性格検査対策方法について知れ、簡単に選考を通過できるようになるので、ぜひ参考にしてください。
就活アドバイザー 京香
「SPIやWebテストの対策どうしよう…」「正直、短時間で点数を上げたい！」という方は、公式LINEで無料配布しているSPI頻出問題集を使うのがおすすめですよ。
SPI頻出問題集では、非言語と言語の頻出問題だけを網羅しているので、練習すれば短期間でボーダーを超えられますよ。
SPIやWebテストの対策を早く終わらせたい方は、ぜひ利用してみてくださいね。
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
（SPI頻出問題集）
「分数 計算」に関するよくある質問
就活生ちゃん
分数の計算方法に関しては知れました。
他に何か知っておくと良いことはありますか？
では、分数の計算に関するよくある質問を2つ紹介します！
就活アドバイザー 京香
- 質問①：分数の計算をする時のコツはある？
- 質問②：分数の計算って電卓を使ってできる？
質問①：分数の計算をする時のコツはある？
分数を計算する時のコツは、分数を単純化しながら計算することです。
分数では通分や掛け算などを繰り返すと、計算過程が複雑になりやすいです。
そのため、分数を単純化、つまり約分しながら計算することで、計算過程を複雑にしすぎず計算できます。
計算ミスをなくし、素早く計算するためにも、分数を単純化しながら計算すると良いでしょう。
質問②：分数の計算って電卓を使ってできる？
分数の計算は電卓でもできます。
そもそも、分数の形は「分子÷分母」という割り算と同じです。
そのため、1/2であれば、電卓で「1÷2」と打ち込むことで計算できます。
電卓を使えるテストであれば、電卓を使って素早く正確に計算しましょう。
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
まとめ：分数の計算に慣れることで、Webテストを確実に突破しよう！
今回は、分数の計算方法を例題と解説を用いながら説明していきました。
他にも、分数を使った確率と割合の問題や、SPIを突破するための勉強法についても解説しました。
この記事を読んだことで、分数の計算やSPIに関する不安や疑問が解消されていたら、嬉しい限りです。