- n進法とはn種類の数を用いて数を表す方法
- n進法を変換する方法は３パターンある
- SPIを突破するためのn進法のおすすめ勉強方法を3つ紹介
- n進法を計算するときのコツは筆算を使うこと
-
Webテストの対策には、以下のツールがおすすめ
-
【就活生/転職者】SPI頻出問題集（LINEで無料配布）
（SPI/Webテストの問題練習） -
【就活生】Lognavi適性診断
（性格テスト90問、SPI練習問題） -
【就活生】適性診断AnalyzeU+
（251問で性格診断、人気No.1）
-
【就活生/転職者】SPI頻出問題集（LINEで無料配布）
この記事では、「n進法の計算方法」や「n進法の練習問題」をご紹介します。
あわせて、「適性検査を突破するためのn進法のおすすめ勉強方法」や「n進法を計算するコツ」についても解説します。
「いつもn進法の問題で躓いてしまう…」という不安が解消されるので、ぜひ最後まで読んでください。
「SPIなどのWebテストで落とされたくない！」という方には「SPI頻出問題集」で実際の問題に近い演習をし、短期間で得点をUPさせるのがおすすめです。
ちなみに「SPI頻出問題集」以外にも、SPI練習問題110問、性格テスト90問ができる「Lognavi適性診断」、251問で性格診断、人気No.1の「適性診断AnalyzeU+」もおすすめですよ。
就活アドバイザー 京香
- 【就活生/転職者】SPI頻出問題集（公式LINEで無料配布）
【公式サイト】https://reashu.com/linelp-spi/
- Webテストで頻出の問題がわかる
- 【就活生】Lognavi（SPI問題が208問：知的118問,性格90問）
【公式サイト】https://lognavi.com/
- テスト結果から最適企業を表示
- 【就活生】適性診断AnalyzeU+（全251問、人気No.1の性格診断）
【公式サイト】https://offerbox.jp/
- 診断でSPI性格検査の練習も
「結局どのサービスを使えば良いかわからない…」という方は「SPI頻出問題集」で練習問題を解いてみるのが一番おすすめですよ。
就活アドバイザー 京香
目次
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
【適性検査対策】n進法の変換をマスターしよう！
就活生ちゃん
Webテストの勉強を始めたのですが、n進法を変換する問題がいつも解けません・・・
n進法の変換はどうやってやれば良いですか？
n進法の問題はコツさえ掴めば簡単にできます！
以下ではn進法の解き方を解説するので、ぜひ参考にしてください！
就活アドバイザー 京香
n進法の変換の基本的な解き方
n進法の変換の基本的な解き方は、nの数字を使って割ったり掛けたりしていきます。
問題のパターンは大きく以下の2つに分かれます。
- 10進数をn進数に変換する問題
- n進数を10進数に変換する問題
いずれのパターンでも、nに当てはまる数字を用いて計算するため、nの数字がいくつでも計算パターンは同じです。
10進数とは、普段私たちの日常生活で使われている表記の仕方です。
私たちは0〜9までの10個の数字で数を表しており、これを10進数と言います。
一方、例えば2進数とは、0と1のみで表記する方法を指します。
中には16進数と言って、数字の0〜9とアルファベットのA~Fまでの16個を使って表記する方法もあります。
下にn進法の変換を例題付きで解説しています！
実戦を踏まえながら練習したい人はそちらも参考にしてください！
就活アドバイザー 京香
n進法は、変換の3パターンを覚えれば大丈夫！
n進法の問題を解くときは、変換の3パターンを覚えていれば大丈夫です。
以下に詳しく解説するので、そちらを参考にしてください。
- ①：10進数からn進数
- ②：n進数から10進数
- ③：n進数からn進数
①：10進数からn進数
10進数からn進数に変換するには、10進数の数をnの数で割り切れなくなるまで割って余りの数を出します。
例えば、95を2進数に変換する時、2で95を割り続けていくと以下のようになります。
95 ÷ 2 = 47 余り 1
47 ÷ 2 = 23 余り 1
23 ÷ 2 = 11 余り 1
11 ÷ 2 = 5 余り 1
5 ÷ 2 = 2 余り 1
2 ÷ 2 = 1 余り 0
1 ÷ 2 = 0 余り 1
余りの数を上から順番に並べたら、2進数での表記となります。
つまり、95を2進数で表すと「1011111」となります。
nに入っている数で割り続ける！
これが10進数からn進数に変換するコツですね！
就活アドバイザー 京香
②：n進数から10進数
n進数から10進数へ変換する時は、n進数で表された数を右から順番にnの0乗、nの1乗･･･と掛けていきます。
例えば、1011111を2進数に変換する時、右から2の0乗、2の1乗･･･とかけていくと以下のようになります。
1 × 2^0 = 1
1 × 2^1 = 2
1 × 2^2 = 4
1 × 2^3 = 8
1 × 2^4 = 16
0 × 2^5 = 0
1 × 2^6 = 64
掛け合わせた数を全て足すと、10進数での表記となります。
つまり、1011111を10進数で表すと「95」となります。
③：n進数からn進数
SPIなど計算の速度が求められる場合は、ｎ進数からｎ進数に変換する方法も是非、覚えておくようにしてください。
ただし、このｎ進数からｎ進数への変換方法は、n進数が2進数・8進数・16進数の場合しか使えないので注意が必要です。
n進数が他のn進数の場合は、一旦10進数に変換した後、目的のｎ進数に変換する必要があります。
例として、2進数1011111を8進数・16進数に変換する方法を以下で紹介します。
①2進数を下1桁から3桁ずつで区切り線を入れる
※桁が足りない場合は0を補充して3桁にする
001 | 011 | 111
②区切った3桁ごとに8進数に置き換える
001 ⇒ 1
011 ⇒ 3
111 ⇒ 7
よって、1011111を8進数に変換した数は137になる。
①2進数を下1桁から4桁ずつで区切り線を入れる
※桁が足りない場合は0を補充して4桁にする
0101 | 1111
②区切った4桁ごとに16進数に置き換える
0101 ⇒ 5
1111 ⇒ F
よって、1011111を16新数に変換した数は5Fになる。
SPIは計算速度が求められることが多いので、2進数・8進数・10進数・16進数の対応は頭に入れておくと良いです。
以下に対応表を載せておくので、ぜひ参考にしてみてください！
就活アドバイザー 京香
| 2進数 | 8進数 | 10進数 | 16進数 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 10 | 2 | 2 | 2 |
| 11 | 3 | 3 | 3 |
| 100 | 4 | 4 | 4 |
| 101 | 5 | 5 | 5 |
| 110 | 6 | 6 | 6 |
| 111 | 7 | 7 | 7 |
| 1000 | 10 | 8 | 8 |
| 1001 | 11 | 9 | 9 |
| 1010 | 12 | 10 | A |
| 1011 | 13 | 11 | B |
| 1100 | 14 | 12 | C |
| 1101 | 15 | 13 | D |
| 1110 | 16 | 14 | E |
| 1111 | 17 | 15 | F |
| 10000 | 20 | 16 | 10 |
「SPIやWebテストの対策どうしよう…」「正直、短時間で点数を上げたい！」という方は、公式LINEで無料配布しているSPI頻出問題集を使うのがおすすめですよ。
SPI頻出問題集では、非言語と言語の頻出問題だけを網羅しているので、練習すれば短期間でボーダーを超えられますよ。
SPIやWebテストの対策を早く終わらせたい方は、ぜひ利用してみてくださいね。
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
（SPI頻出問題集）
【例題あり】n進法の変換の練習問題と解説
就活生ちゃん
n進法の基本的な解き方が分かりました。
良かったです！
練習問題も解いてみましょう。
就活アドバイザー 京香
- 問題①② : 10進法からn進法に変換する問題
- 問題③④ : n進法から10進法に変換する問題
- 問題⑤⑥ : n進法からn進法に変換する問題
- おまけ : 少数を含むn進法の変換の問題
10進数からn進数に変換する問題①
10進数からn進数に変換する問題1つ目は、「10進数の45は2進数で表すといくつか？」です。
以下で解答を載せていますが、まずは自分で解いてみましょう！
10進数から2進数の変換は、10進数45の数を2で割った時の商が0もしくは1になるまで割り続け、その時の最後の商、さらに余りの数を下から順に並べた数が2進数の値になります。
45 ÷ 2 = 22 余り 1
22 ÷ 2 = 11 余り 0
11 ÷ 2 = 5 余り 1
5 ÷ 2 = 2 余り 1
2 ÷ 2 = 1 余り 0
1 ÷ 2 = 0 余り 1
よって、45を2進数で表すと101101となります。
10進数からn進数に変換する問題②
10進数からn進数に変換する問題2つ目は、「10進数の574をn進数で表すと2354になった。これは何で表した値か？」です。
以下で解答を載せていますが、まずは自分で解いてみましょう！
変換後の数値が2354なので、2進数、3進数、4進数、5進数という選択肢はなくなります。
元々の数が574なので、2354は10進数で表した数値ではありません。
よって、解答は6進数、7進数、8進数、9進数のいずれかになります。
順番に変換して2354になる進数を探すしかないのですが、6進数から順番に計算してはいけません。
そうするとすると9進数が答えだった場合、4回計算しなければならないことになります。
しかし、間の7進数もしくは8進数から計算することで計算が少なく済みます。
n進数のnが小さいほど桁上がりが早く発生し、桁数が大きくなります。
よって、7（8）進数に変換した数値が2354より大きい（小さい）場合、その時点で解答が8進数もしくは9進数（6進数もしくは7進数）だと確定します。
逆に７（8）進数に変換した数値が2354より小さかった（大きかった）場合、6（9）進数が解答になることがわかります。
では、10進数574を7進数に変換します。
574 ÷ 7 = 82 余り 0
82 ÷ 7 = 11 余り 5
11 ÷ 7 = 1 余り 4
1 ÷ 7 = 0 余り 1
よって、574を7進数で表すと1450となります。
n進数から10進数に変換する問題①
n進数から10進数に変換する問題1つ目は、「3進数1201を10進数で表すといくつになるか？」です。
以下で解答を載せていますが、まずは自分で解いてみましょう！
3進数から10進数の変換は、3進数の1桁目から3の0乗、3の1乗、3の2乗・・・と順にかけて更に各桁を足します。
1 × 3^0 = 1
0 × 3^1 = 0
2 × 3^2 = 18
1 × 3^3 = 27
よって、各桁を足すと46となります。
n進数から10進数に変換する問題②
n進数から10進数に変換する問題2つ目は、「6進数3420を10進数で表すといくつになるか？」です。
以下で解答を載せていますが、まずは自分で解いてみましょう！
6進数から10進数の変換は、6進数の1桁目から6の0乗、6の1乗、6の2乗・・・と順にかけて更に各桁を足します。
0 × 6^0 = 0
2 × 6^1 = 12
4 × 6^2 = 144
3 × 6^3 = 648
よって、各桁を足すと804となります。
n進数からn進数に変換する問題①
n進数からn進数に変換する問題1つ目は、「5進数3420を2進数で表すといくつになるか？」です。
以下で解答を載せていますが、まずは自分で解いてみましょう！
5進数3420を2進数に変換する場合は、一旦10進数に変換した後に2進数に変換します。
5進数から10進数の変換は、5進数の1桁目から5の0乗、5の1乗、5の2乗・・・と順にかけて更に各桁を足します。
0 × 5^0 = 0
2 × 5^1 = 10
4 × 5^2 = 100
3 × 5^3 = 375
よって、各桁を足すと485となります。
これを2進数に変換します。
485 ÷ 2 = 242 余り 1 242 ÷ 2 = 121 余り 0 121 ÷ 2 = 60 余り 1 60 ÷ 2 = 30 余り 0 30 ÷ 2 = 15 余り 0 15 ÷ 2 = 7 余り 1 7 ÷ 2 = 3 余り 1 3 ÷ 2 = 1 余り 1 1 ÷ 2 = 0 余り 1
よって5進数3420を2進数で表したものは、111100101になります。
n進数からn進数に変換する問題②
n進数からn進数に変換する問題2つ目は、「7進数5620を4進数で表すといくつになるか？」です。
以下で解答を載せていますが、まずは自分で解いてみましょう！
7進数5620を4進数に変換する場合は、一旦10進数に変換した後に4進数に変換します。
7進数から10進数の変換は、7進数の1桁目から7の0乗、7の1乗、7の2乗・・・と順にかけて更に各桁を足します。
0 × 7^0 = 0
2 × 7^1 = 14
6 × 7^2 = 294
5 × 7^3 = 1715
よって、各桁を足すと2023となります。
これを4進数に変換します。
2023 ÷ 4 = 505 余り 3
505 ÷ 4 = 126 余り 1
126 ÷ 4 = 31 余り 2
31 ÷ 4 = 7 余り 3
7 ÷ 4 = 1 余り 3
3 ÷ 4= 0 余り 1
よって7進数5620を4進数で表したものは、133213になります。
おまけ：小数を含むn進法の変換
おまけとして、小数を含むn進数の変換の方法についても紹介します。
n進数での小数点以下の位は、小数第1位から順に、
1 / n , 1 / n^2, 1 / n^3 , ・・・
となります。
例えば0.32（4）の時は、
| 1 / 4^1 | 1/ 4^2 |
| 3 | 2 |
よって上下を掛け合わせて足すと、
1 / 4^1 × 3 ＋ 1 / 4^2 × 2
＝ 3/4 + 1/8
＝ 7/8
＝ 0.875
これより、10進法で表すことができます。
例えば、0.856を5進数で表す時は、小数部分のみに部分のみに5を掛け算していきます。
0.856 × 5 = 4.280
整数部分は4、小数部分は0.28であることにより、
0.28 × 5 = 1.40
整数部分は1、小数部分は0.4であることにより、
0.4 × 5 = 2.0
整数部分は2、小数部分は0となります。
このように小数部分が0になるまで続けます。
解答する際には、
①元の数の整数部分を先頭の1の位とする
②掛け算した結果の整数部分を順に小数点以下の数として書き並べる
したがって、5進数で表すと0.412（5）となります。
ここで、小数を含むn進数の変換の練習問題を紹介します。
以下で解答を載せていますが、まずは自分で解いてみましょう！
問題 : 16進法における3DA.F8（16）を10進数で表すといくつか？
上で紹介した通り行うと、
3 × 16^2 ＋ 13 × 16^1 + 10 × 16^0 + 15 / 16 + 8 / 16^2
＝31583 / 32
＝986.96875
と計算できます。
n進法の基礎から応用まで学べましたね。
しっかり計算の仕方を習得しましょう！
就活アドバイザー 京香
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
適性検査を突破するためのn進法の変換のおすすめ勉強法
就活生ちゃん
n進法の練習問題が解けるようになってきました。
n進法の変換のおすすめの勉強方法があれば教えて欲しいです！
分かりました！
では以下でおすすめの勉強方法について紹介します。
就活アドバイザー 京香
- その① : 問題集を繰り返し解き、解き方のパターンを覚える
- その② : ただ暗記をするのではなく、考え方を理解しておく
- その③ : 問題に慣れてきたら、時間配分も意識して解いてみる
その①：問題集を繰り返し解き、解き方のパターンを覚える
n進法の変換のおすすめの勉強方法1つ目は、「問題集を繰り返し解き、解き方のパターンを覚える」です。
「n進法」と聞くと一見難しいような印象を受けるかもしれませんが、n進法は問題のパターンが限られているため対策すれば誰でも確実に得点できます。
そのため、演習を重ねることで安定して点数が取れるようになると思われます。
以下でSPIのn進数のおすすめの参考書を紹介します。
「就職適性検査の非言語分野がスッキリわかる本 n進法, 数列編 （かんべやすひろ 著）」
この本は、数学が苦手な学生にも分かりやすいように丁寧に解説がされています。
Webテストに出題される中でも、n進法と数列に特化した本になっているので効率よく学習を進めることができます。
つまずく学生が多いポイントに基づいた丁寧な解説がされているので、理解を深めることができるでしょう。
その②：ただ暗記をするのではなく、考え方を理解しておく
n進法の変換のおすすめの勉強方法2つ目は、「ただ暗記をするのではなく、考え方を理解しておく」です。
n進法に限った話ではないですが、解き方を暗記していても全ての問題には対応できません。
暗記していない問題が出た場合、解き方が分からず困ってしまいます。
なので、なぜこの解き方をするのかをしっかり理解し、見たことがない問題が出たとしても臨機応変に対応できるようにしましょう。
解き方を丸暗記するのではなく、なぜそのように解くのか理解しておくことが大切です！
就活アドバイザー 京香
その③：問題に慣れてきたら、時間配分も意識して解いてみる
n進法の変換のおすすめの勉強方法3つ目は、「問題に慣れてきたら、時間配分も意識して解いてみる」です。
Webテストの制限時間は問題数から見るとかなり少なく、途中で時間切れになってしまう人も多くいます。
そのため、制限時間内に全ての問題を解ききる練習は必須といえます。
分野ごとに目標時間を決め、その時間配分を意識して解いてみることがWebテスト突破の近道になります。
テスト本番はいつもよりも緊張すると思います。
そのような時でもいつも通りのパフォーマンスを出すために、普段から時間内に解ききる練習をしておきましょう！
就活アドバイザー 京香
よくある適性検査の対策に役立つ記事一覧
就活アドバイザー 京香
「SPIやWebテストの対策どうしよう…」「正直、短時間で点数を上げたい！」という方は、公式LINEで無料配布しているSPI頻出問題集を使うのがおすすめですよ。
SPI頻出問題集では、非言語と言語の頻出問題だけを網羅しているので、練習すれば短期間でボーダーを超えられますよ。
SPIやWebテストの対策を早く終わらせたい方は、ぜひ利用してみてくださいね。
就活アドバイザー 京香
- 言語・非言語両方の頻出問題が網羅されている
- 二字熟語90選/四字熟語50選で言語の対策がしっかりとれる
- 実際の問題に近い演習ができる
（SPI頻出問題集）
「n進法の変換」に関するよくある質問
就活生ちゃん
n進法の変換の勉強方法がよく分かりました！
最後にn進法の変換について、何か知っておいた方がいいことはありますか？
それでは最後に、n進法の変換に関するよくある質問について3つご紹介します！
就活アドバイザー 京香
- 質問① : n進法の変換ができるサイト・計算機ってある？
- 質問② : n進法の裏技を知りたい！
- 質問③ : SPIでn進法の問題は出題されるの？
質問①：n進法の変換ができるサイト・計算機ってある？
n進法の変換に関するよくある質問1つ目は、「n進法の変換ができるサイト・計算機ってある？」です。
結論から言うと、n進法の変換ができるサイト・計算機はあります。
ネットで検索すると複数のサイトが出てきます。
サイトの中には2進数から36進数と幅広く変換に対応しているものもあるので、ぜひ使ってみてください。
n進法の変換ができるサイト・計算機は便利ですが、本番は自力で解くことになります。
そのため自分で計算して答えを合わす練習もしておきましょう。
就活アドバイザー 京香
質問②：n進法の計算の裏ワザを知りたい！
n進法の変換に関するよくある質問2つ目は、「n進法の計算の裏技が知りたい！」です。
n進法の裏技としてよく知られているのは、筆算でのn進法の変換です。
この筆算での変換は10進数からn進数への変換の際に使うことができます。
筆算での方法は以下のようになります。
これは35を2進数で表すと言う問題の場合です。
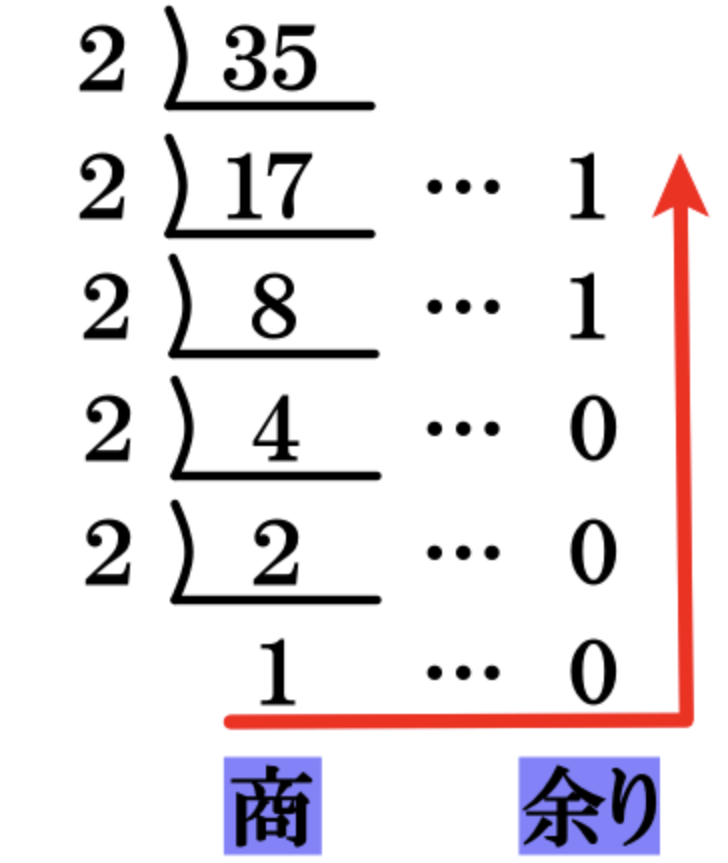
参照 : 遊ぶ数学
2進数で表すために元の数を商が1になるまでわり続け、そこから逆L字に並べたものが２進数で表した数値になっています。
この方法は計算が機械的にできるので、時間短縮に繋がるのでおすすめです。
質問③：SPIでn進法の問題は出題されるの？
n進法の変換に関するよくある質問3つ目は、「SPIでn進法の問題は出題されるの？」です。
結論から言うと、SPIでn進法の問題は出題されないようです。
というのも、SPIでは中学・高校で学習される内容をもとにして問題が出題されますが、n進法は平成14年度の学習指導要領の改訂によって学習項目から削除されてしまいました。
しかし、平成24年度の学習指導要領の改訂によってn進数は再び高校の数学Aでの学習項目に追加されました。
これによりn進数を学習せずに中学・高校を卒業した人が多数いるため、SPIでは出題範囲に含まれていないようです。
「SPIを短時間で対策」「もっといろんな問題を解いて試験に慣れたい！」なら、就活の教科書公式LINEから誰でも無料で受け取れる「SPI頻出問題集」がおすすめです。
SPI頻出問題集は、豊富な言語・非言語問題と丁寧な解説付きなので、練習すればSPIやWebテストで高得点を狙えます。
「実際の問題と類似してる点が多く、非常に役立ちました。」との口コミがあるように、本番のテストに近い問題や、多くの就活生が苦手としている二字熟語、四字熟語の頻出まとめなどもわかります。
点数が一気に伸びた人も多いので、ぜひ公式LINEからGETしてみてくださいね。
（SPI頻出問題集）
まとめ：方程式の計算に慣れることで、適性検査を突破しよう！
今回はn進法の計算方法について解説しました。
あわせて、n進法の練習問題、Webテストを突破するためのn進法のおすすめの勉強方法、n進法を計算する時のコツについてもご紹介しました。
この記事を読んだことで、n進法の計算方法に関する不安や疑問が解消されていたら、嬉しい限りです。