まずは、SPI頻出問題集をご覧いただきありがとうございます!
65%以上の企業が採用していると言われ、就職活動の際に必ずといっていいほど受験するのがSPIです。
しかし、SPI対策というと過去問や参考書を紹介されることが多く、正直ハードルが高くめんどくさいですよね・・・
そこで、おすすめなのがアプリだけで簡単にSPI対策ができる「Lognavi」です。
Lognaviは無料のアプリで簡単にSPI対策ができるだけでなく、「適性検査」の対策まで一緒にできるので、まだ登録していない人はぜひ試してみてくださいね!
~はじめに~SPIについて

SPIとは、リクルートマネジメントソリューションズが提供する、応募者の能力や人柄を把握する目的で行われる適性検査です。
SPIの適性検査の内容としては、以下の2つで構成されています。
● 適性検査:人柄や行動特性を図る検査
● 能力検査:学力や知的能力を測る検査
適性検査では、日常の行動や考え方について複数の質問項目が提示され、どの程度自分にあてはまるかを選択していきます。
能力検査では、「言語分野」と「非言語分野」の2種類の問題を通して、コミュニケーションや思考力、新しい知識・技能の習得などのベースとなる能力を測ります。
~第1章~適性検査

SPIの適性検査で重要なポイントは、エントリーシートや面接と一貫性があることです!
例えば、適性検査と面接で一貫性がないと面接官に「言っていることに矛盾があるな」と思われてしまい、選考の通過率が下がってしまいます。
なので、SPIを受ける前に軽く適性検査を練習しておくことをオススメします!
以下の診断は無料なので、ぜひSPIの適性検査対策に使ってくださいね!
- ポイント①:アプリで簡単にSPI対策ができる
- ポイント②:SPIでの自分の「偏差値」がわかる
- ポイント③:テスト結果を見た企業からスカウトが来る
SPIなどのWebテストの対策方法としておすすめなのが、「Lognavi」です。
Lognaviでは、あなたの知力を測れる独自の知的テスト・自己分析に役立つ性格検査を受けられます。
知的テストでは、言語力・計算応用力などの系統別の能力も測れるため、SPIやWebテストの対策には大変おすすめです。
 就活アドバイザー 京香
就活アドバイザー 京香
Lognaviはアプリで簡単にSPI対策ができる上に、自分が就活生の中でどれくらいの立ち位置なのかも診断してくれます。
SPIの対策がまだ完璧でない人は、ぜひ使ってみてくださいね!
 就活アドバイザー 京香
就活アドバイザー 京香
自分の詳しい適性を知って、適職を見つけよう【適性診断AnalyzeU+】
①:前251問の質問で、あなたの適性を客観的に診断!
②:28項目から、自分のアピールすべき強みがわかる!
③:診断結果を見た企業が、あなたの人となりを見てスカウト!
自己PRで使えるような強みが見つからないとお困りの方は、適性診断AnalyzeU+がおすすめです!
全251問の圧倒的な質問量で、あなたの強み・適性を客観的に診断してくれるんです!
 就活アドバイザー 京香
就活アドバイザー 京香
適性診断AnalyzeU+は、単に診断を受けるだけでなく、企業からのスカウトにもつながるんです!
そのうえ、自己PRを書く上でのアドバイスももらえるので、ぜひ一度診断を受けてみてくださいね!
 就活アドバイザー 京香
就活アドバイザー 京香
あらかじめ自分の強みを把握できる(キャリアチケット就職スカウト)
「自分の適性検査結果を知っておきたい」という方は、キャリアチケット就職スカウトで適性診断してみてください!
例えば、キャリアチケット就職スカウトは、本番の適性検査の前に、あらかじめ自分の強みを知っておくことができます。
 就活アドバイザー 京香
就活アドバイザー 京香
①:適性検査によって、あらかじめ自分の強みがわかる
②:企業を無理に探さなくても、気の合う企業に効率よく出会えるので、納得の企業から内定がもらえる
③:オファーをもらうといきなり企業と連絡を取り選考に進めるから、早く就活が終わる
キャリアチケット診断では、診断によってあなたの価値観がはっきりとわかります。
さらに、あなたの価値観に共感した優良企業からオファーが来るので、大手のナビサイトからエントリーするよりもはるかに内定をゲットしやすいですよ。
「企業選びに失敗したくない」「有利に就活を進めたい」という就活生は、さっそく利用してみましょう。
 就活アドバイザー 京香
就活アドバイザー 京香
~第2章~非言語

非言語①:図形を使った問題
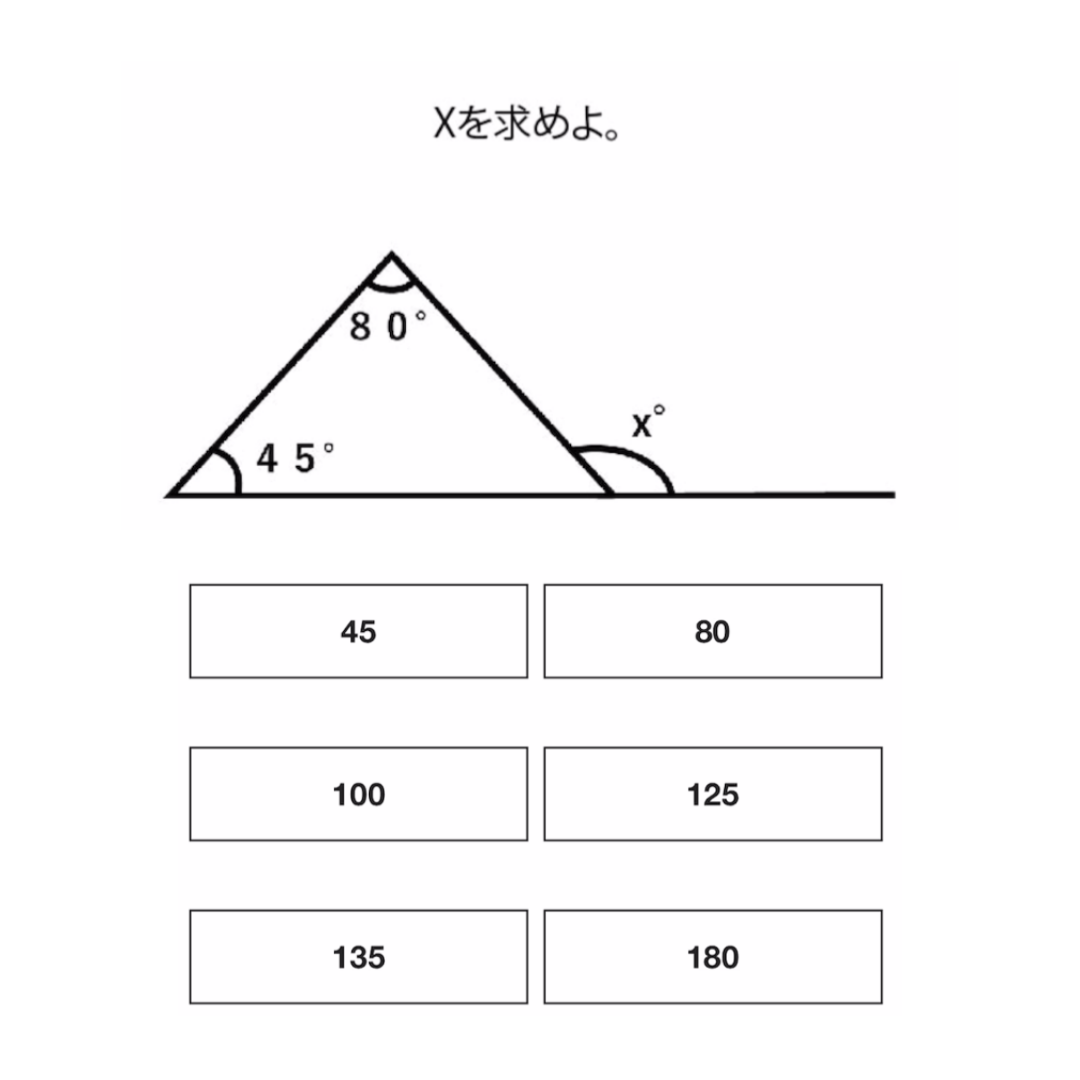
この図形問題は、「三角形の内角と外角の関係」を理解していれば、すぐに解ける問題です。
「三角形の1つの外角は、隣り合っていない2つの内角の和に等しい」という法則があります。
そのため、この場合は内角の和が「80+45=125」、外角であるxの角度は「125度」であることがわかります。
 就活アドバイザー 京香
就活アドバイザー 京香
この図形に色を塗りたい。 赤、青、黄、緑の4色が使えるとき、色の塗り方は何通りか。 ただし、船で隣り合う領域には同じ色が使えないものとする。
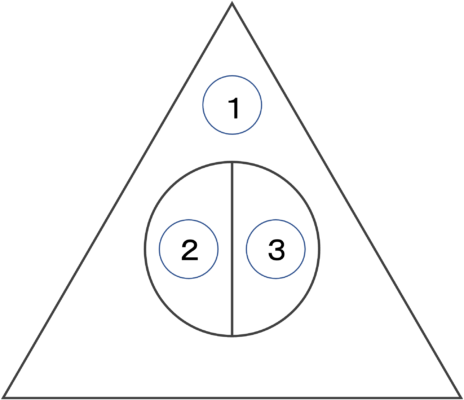
①に塗る色は4色のうち1色なので、4通り。
すると、②に塗る色は残りの3色から1色なので、3通り。
すると、③に塗る色は残りの2色から1色なので、2通り。
したがって、4×3×2=24通り
「別解」
4色から3色を選んで、図の①、②、③の3カ所に色を塗るので、
4P3=24通り
次の3つの指揮によって示される放物線と直線は、下図のように平面を8つの領域で分ける。 次の2式からなる連立不等式で表される領域はどれか。
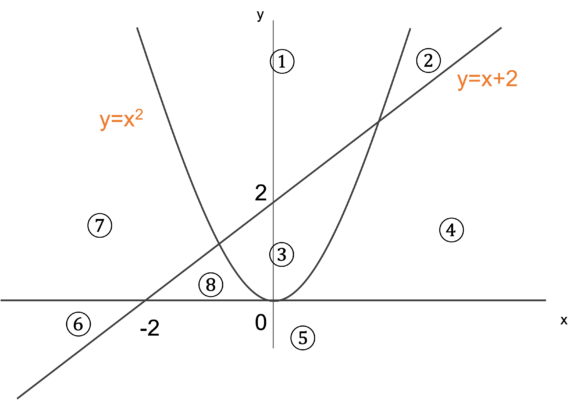
不等式がyに対して開いていれば、yの値の方が大きいので、上の領域。
不等式がyに対して閉じていれば、yの値の方が小さいので、下の領域。
すると、y>x^2の範囲は以下の通り。
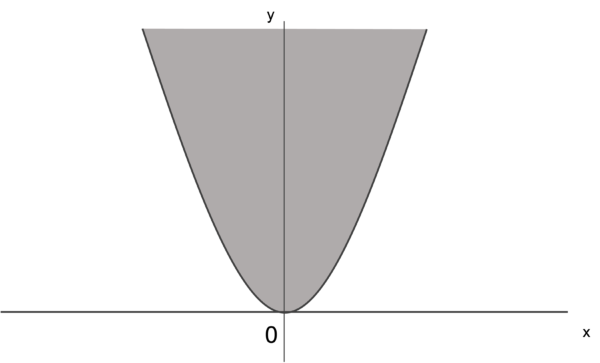
また、y<x+2の範囲は以下の通り。
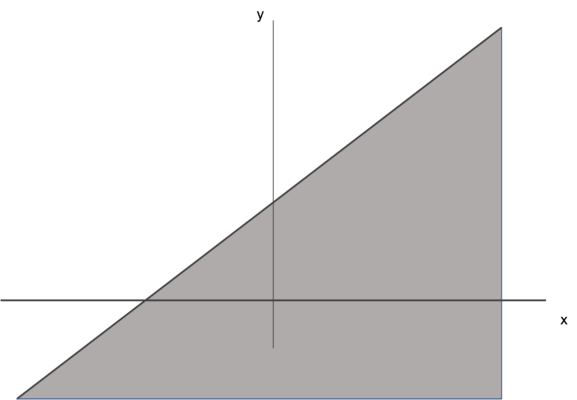
これら2つの領域が重なっている部分が求める領域なので、③
外国人200人にアンケートを行ったところ、英語が話せる人は120人、フランス語が話せる人は40人、ドイツ語が話せる人は60人いた。 英語とフランス語の両方が話せる人が25人いた。 英語とフランス語のどちらか片方だけ話せる人は何人か。 ただし、ドイツ語は関係ないものとする。
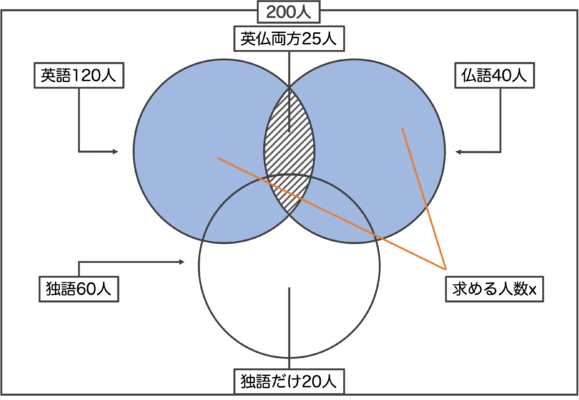
英語と仏語の両方が話せる25人は斜線部分。
求める「英語と仏語のどちらか片方だけ話せる人」は上図の青い部分。
英語だけ→12-25=95人
仏語だけ→40-25=15人
合計 →95+15=110人
P市、Q市、R市の人口密度(1km^2あたりの人口)を下表に示してある。 P市とR市の面積は等しく、Q市の面積はP市の2倍である。 次の推論ア、イの正誤を考えなさい。
市
人口密度
P
390
Q
270
R
465
「P市とR市の面積は等しく、Q市の面積はP市の2倍」なので、
仮にP市とR市の面積を1km^2、Q市の面積を2km^2と考える。
アについて、
Q市の人口は、270×2=540人
R市の人口は、465×1=465人
2つの死を合わせた地域の面積は3km^2なので、人口密度は、
(540+465)÷3=335
になるので、300ではない。
よって、アは誤り。
イについて、
Q市の人口は540人、R市は465人なので、Q市の方が多い。
よって、イは正しい。
空欄に当てはまる選択肢を1つ選び、図形群の法則性を完成させなさい。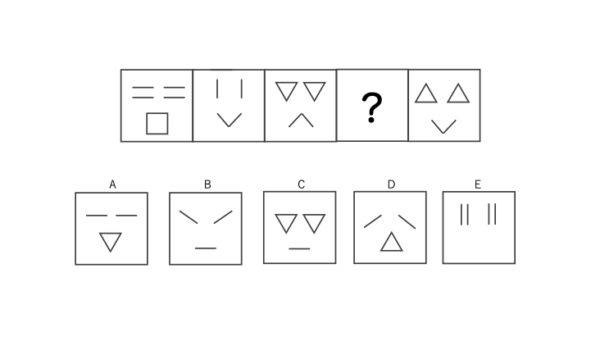
左から右に考える
法則性:図形を構成する線の数が「8本⇄4本」を繰り返す
非言語②:推論
P、Q、R、S、Tの5つの支店の売上高を比較した。 5つの支店について次のことが分かっている。 次のア、イ、ウの推論のうち、必ず正しいものはどれか。
A:アだけ
B:イだけ
C:ウだけ
D:アとイの両方
E:アとウの両方
F:イとウの両方
G:アとイとウのすべて
H:必ず正しい推論はない
順位を推論する問題は、想定できる順位のパターンを全て洗い出す。
下記のルールにしたがって、与えられた情報を図式化する。
「順位の高低関係のみ」を表現するときは、「[ 順位がより高い方 ] > [ 順位がより低い方 ]」と表す。
「連続する順位の並び」を表現するときは、「[ 順位が高い方 ] → [ 順位が低い方 ]」と表す。(ただし、この問題では使わない。)
このルールにしたがって、問題文の情報を図式化する。
ⅰ)「Rの順位は、Sより上である」より、RとSの順位関係は、「R > S」・・・①
ⅱ)「Tの順位は、Rよりも上だが、1着ではなかった」より、TとRの順位関係は、「□ > T > R」・・・②
①、②より、「□ > T > R > S」・・・③
ⅲ)「Qの順位は、Pより上である」より、「Q > P」・・・④
③、④より、考えられる順位は、次の4通りである。
| 順位 | |||||
| 1位 | 2位 | 3位 | 4位 | 5位 | |
| パターン1 | Q | P | T | R | S |
| パターン2 | Q | T | P | R | S |
| パターン3 | Q | T | R | P | S |
| パターン4 | Q | T | R | S | P |
ここで、推論ア~ウについて考えると
表より、1位はQである。よって、ア「Qは1位である」は必ず正しい。
表より、5位はSかPである。よって、イ「Sは5位である」は正しいとは限らない。
表より、2位はPまたはTである。よって、ウ「2位はPまたはTである」は必ず正しい。
したがって、正しい推論はアとウの両方。
A市、B市、C市の人口密度(面積1km2当たりの人口)は下表の通りである。 A市とB市の面積は等しく、それぞれC市の面積の半分である。 次のア、イの正誤を考え、AからIまでの中から正しいものを1つ選びなさい。
市
人口密度
A
200
B
160
C
120
面積を仮定して、それぞれの市の人口を計算していきましょう。
A市とB市の面積は等しく、それぞれC市の面積の半分であることから、
A市の面積を1 km2と仮定すると、B市の面積は1 km2、C市の面積は2 km2となります。
それぞれの市の人口は、
A市の人口:200 × 1 = 200 人
B市の人口:160 × 1 = 160 人
C市の人口:120 × 2 = 240 人
(アについて)
A市の人口200人は、C市の人口240人よりも少ないので、記述は正しいです。
(イについて)
B市とC市を合わせた人口は、160 + 240 = 400 人
B市とC市を合わせた面積は、1 + 2 = 3 km2
よって、B市とC市を合わせた人口密度は、400 / 3 = 133.3 人/ km2
したがって、A市の人口密度200人/ km2より少ないため、記述は誤りです。
ジョーカーを含まない52枚1組のトランプから、カードが1枚配られた。 この1枚のカードについて、A、B、Cの3人から次の発言があった。 3人の発言は信頼できるとは限らない。そこで、いろいろな場合を想定して推論がなされた。 (1)次のア、イ、ウの推論のうち、正しいのはどれか。
ア、イ、ウの推論を順番に検証していきましょう。
- (アについて)「 Aさんが正しければ、Bさんも必ず正しい」
Aさんが正しい場合、カードはハートの8以外の51枚のどれかになります。
例えば、ハートの5や、スペードの10などの場合が考えられます。
Bさんは「ハートではない」と発言していますが、8以外のハートの可能性があるため、必ず正しいとは限りません。
よって、アの推論は誤りです。
- (イについて)「Bさんが正しければ、Cさんも必ず正しい」
Bさんが正しい場合、カードはハート以外のスペード、クローバー、ダイヤのどれかになります。
例えば、スペードの5やダイヤのAなどの場合が考えられます。
Cさんは「スペードの8である」と発言していますが、Bさんの発言からは、必ず「スペードの8」であるとは言えません。
よって、イの推論は誤りです。
- (ウについて)「Cさんが正しければ、Aさんも必ず正しい」
Cさんが正しい場合、このカードはスペードの8の1つに特定されています。
この時、Aさんの「ハートの8ではない」の発言は矛盾がありません。
よって、ウの推論は正しいです。
以上から、ウの推論のみが正しいとするCが正解となります
P、Q、R、Sの4チームが、サッカーの試合を総当たり戦で行った。その試合結果について、次のことが分かっている。 次のア、イ、ウの推論のうち、必ずしも誤りとはいえない推論はどれか。
対戦成績の問題では、総当たり戦の表を作成して考えると良いです。
ii) iii) iv) の情報から、対戦表は次のようになります。
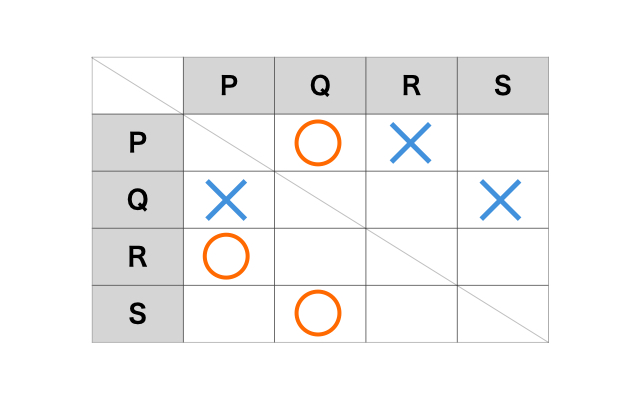
i)で「Pは1勝2敗である」ので、PはSに負けたことがわかります。
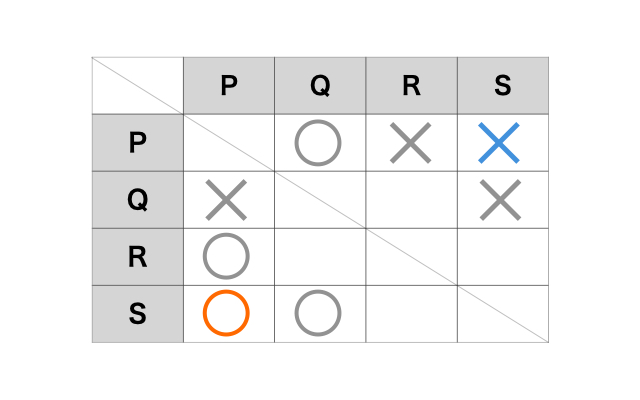
i) ~ iv)の情報から分かることは、ここまでです。
この状態でv)を満たすように空欄を埋めたときに、ア、イ、ウのそれぞれが成り立つ場合があるかを検証していきましょう。
- (アについて)「Qは1勝2敗だった」
QがRに勝った場合には、アの推論は正しくなります。
- (イについて)「Rは全勝だった」
RがQとSの両方に勝った場合に、イの推論は正しくなります。
- (ウについて)「Sは1勝2敗だった」
Sは既に2勝しているので、SとRの結果によらず、ウの推論は誤りです。
以上から、アとイの両方が正しいとしているDが正解となります
次のア、イの正誤を考え、AからIまでの中から正しいものを1つ選びなさい。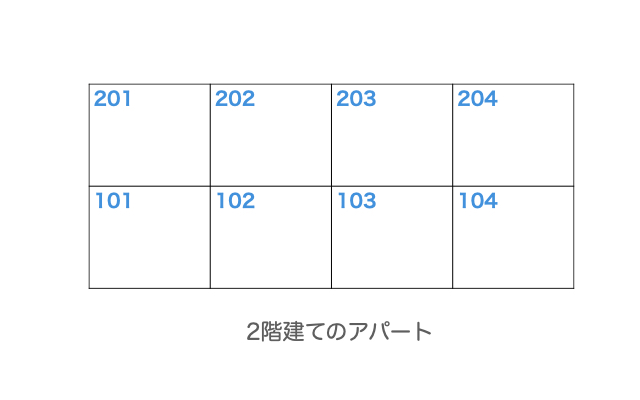 上図のような2階建てのアパートに、A、B、C、D、E、Fの6人が1人1部屋で住んでいて、次のことが分かっている。
上図のような2階建てのアパートに、A、B、C、D、E、Fの6人が1人1部屋で住んでいて、次のことが分かっている。
条件を整理しながら、位置を埋めていきましょう。
i) Aは104号室に住んでいる
ii) Bの真上にはCが住んでいる
iv) Eの左隣にはFが住んでいる
の条件を図で整理すると、下のようになります。
ii)やiv)のような、入る場所が分からないが、位置関係が分かるものは、1つのブロックのように扱うと考えやすくなります。
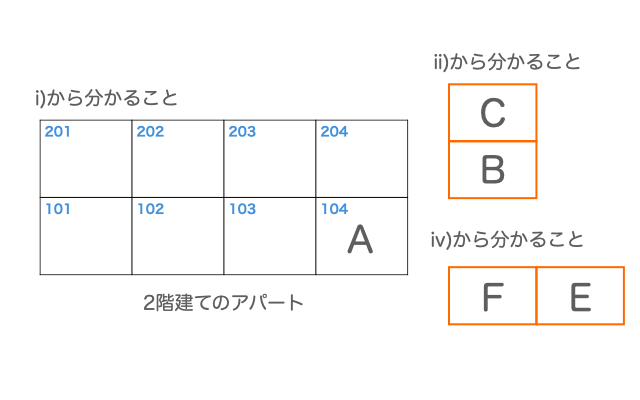
C、Bのブロックの入れ方に着目すると、次の3つのパターンが考えられます。
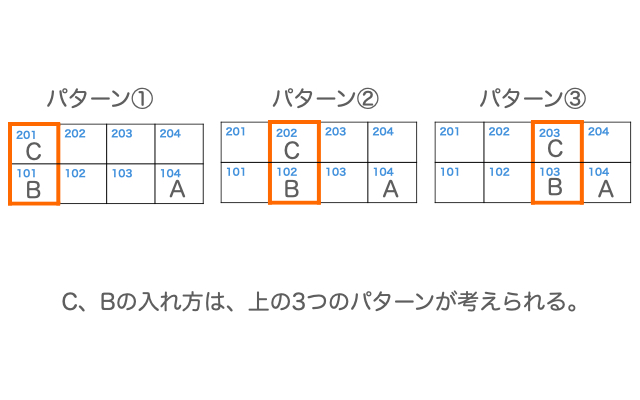
それぞれのパターンについて、F、Eの入れ方、Dの入れ方を考え、条件を満たすかを検証していきます。
パターン①の場合、パターン①-1、パターン①-2が条件を満たします。
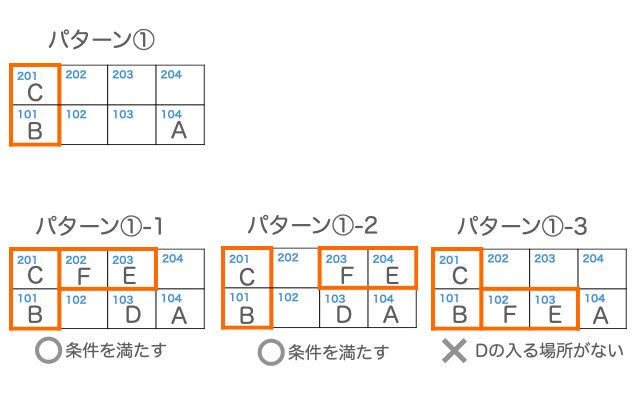
パターン②の場合、iii)の条件を満たすように、Dを入れることができないので、不適となります。
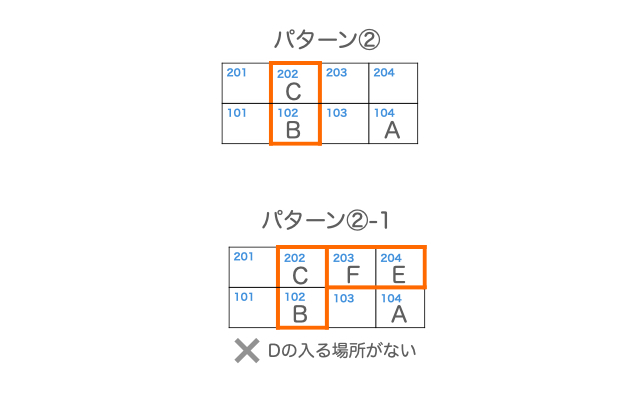
パターン③の場合、v)の条件を満たすように、F、Eを入れることができないので、不適となります。
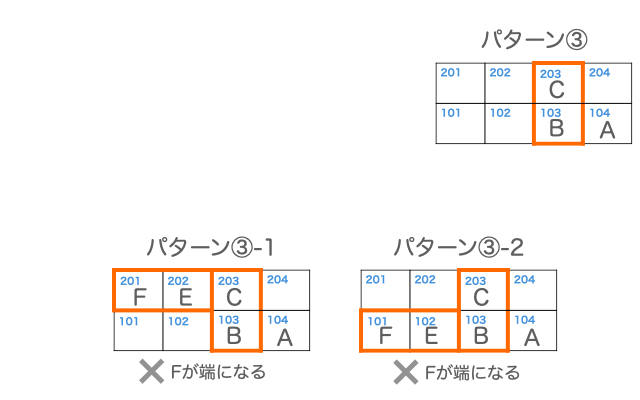
以上から、想定される位置関係は、パターン①-1、パターン①-2のいずれかであることがわかります。
ア) Aの真上は、パターン①-2の場合は、空き家ではないので、推論は誤りです。
イ)Dの右隣は、パターン①-1、パターン①-2のいずれもAなので、推論は正しいです。
したがって、「D:アは誤りだが、イは正しい」が正解となります。
A、B、Cの3つの商品があります。 これらの商品の価格について、次のことがわかっています。 このとき、次のア、イ、ウの推論のうち、必ず正しいものはどれか?
A、B、Cの価格を比較するので、合計値を求めてみます。
「AとBの価格の平均額は、900円である」ので、AとBの価格の合計は
- A + B = 900 × 2 = 1800 ・・・①
「BとCの価格の平均額は、600円である」ので、BとCの価格の合計は、
- B + C = 600 × 2 = 1200 ・・・②
① – ②を考えると、
A – C = 600
となるので、AはCより600円高いことがわかり、Aは600円以上であることが確定します。
ここから、推論を順番に検証します。
(アについて) 「Bの価格は、Aの価格より高い」
AとBの合計が1800円であり、Aが600円以上という条件から、
例えば、Aが1000円、Bが800円の場合、不適となります。
よって、アは誤りです。
(イについて)「Cの価格は、Aの価格より高い」
AはCより600円高いという条件から、CがAより高くなることはありません。
よって、イは誤りです。
(ウについて)「Cの価格は、Bの価格より高い」
例えば、Cの価格を100円とすると、A = 700円、B = 1100円となり、これは式を満たします。
よって、Cの価格がBの価格よりも安い場合もな成り立つので、ウは誤りです。
以上から、「H:必ず正しい推論はない」が正解です
青玉、黄玉、赤玉が合わせて7個あります。 それぞれの個数について次のことが分かっています。 次のア、イ、ウの推論のうち、必ず正しいものはどれか。
まず、条件i、iiより、4個の玉の内訳は、次のようになります。
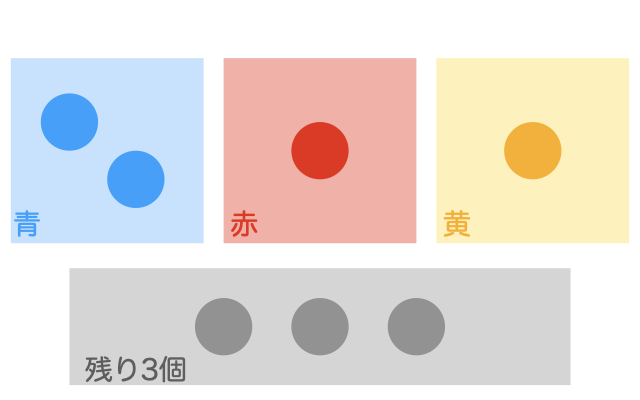
よって、残りの3個の玉の内訳を考えればよいです。
推論を順番に検証していきましょう。
(アについて)「青玉が3個であれば、黄玉は2個である」
黄玉は青玉より少ないので、青玉が3個のとき、黄玉は2個か1個です。
黄玉が1個の場合もあり得るので、アは必ず正しいとは言えません。

(イについて)「黄玉が2個であれば、赤玉は1個である」
黄玉が2個のとき、青玉は3個か4個になります。
青玉が3個のとき、赤玉は2個となるので、イは必ず正しいとは言えません。

(ウについて)「赤玉が3個であれば、青玉は3個である」
赤玉が3個のとき、残る玉は4個ですが、青玉が黄玉よりも多くなる内訳は、青玉3個、黄玉1個の場合のみです。
よって、ウは必ず正しいと言えます。

以上より、「C:ウだけ」が正解です。
非言語③:順列・組み合わせ
ある企業の新卒採用の面接の1日目と2日目の面接官を、A、B、C、Dの4名のうちから1名ずつ選ぶ。 1日目と2日目が同じ人にならないように選ぶとすると、選び方は何通りあるか。
1日目の面接官から考えると、1日目の面接官はA、B、C、Dの4名すべてなり得る。
つまり、4通り。
2日目は、1日目に選ばれた人以外の3人から1人選ぶことになる。
つまり、3通り。
したがって、
4×3=12(通り)。
P、Q、R、S、T、Uの6人で、円形のテーブルに座る。 PとQが隣同士になるように6人が座る座り方は何通りか。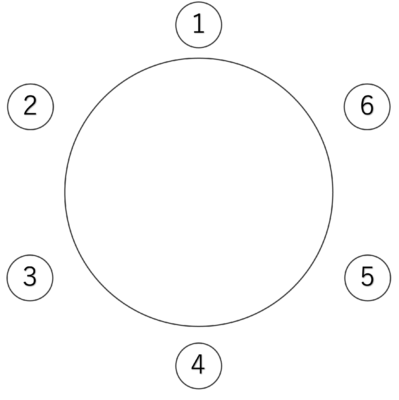
問題文に「隣り合わせになるように」とある場合は、それらを1つの塊だと考えてから、さらにその中での場合分けを考えます。
隣り合う2席は、①②、②③、③④、④⑤、⑤⑥、⑥①の6通り。
また、PQの座り方はそれぞれに(P・Q)、(Q・P)の2通りがある。
よって、6×2=12通り。
残りの4席の決め方は、4!=4×3×2×1=24通り。
これらを掛け合わせて、12×24=288通り。
X組とY組の生徒が5人ずつ、合わせて10人いる。 この中から掃除当番を4人選びたい。 X組の生徒が3人、Y組の生徒が1人となるように選ぶとすると、掃除当番の選び方は何通りあるか。
X組の生徒の選び方は、
5C3=(5×4×3)/(3×2×1)=10通り
Y組の生徒の選び方は、5通り
したがって、
10×5=50通り
X組とY組の生徒が5人ずつ、合わせて10人いる。 この中から掃除当番を4人選びたい。 X組の生徒が少なくとも1人含まれるように選ぶとすると、掃除登板の選び方は何通りあるか。
問題文に「少なくとも」とある時は、「問題文と反対の場合の数」を「全体の場合の数」から引きます。
X組の生徒が1人も含まれない選び方を考えると、
X組0人、Y組4人の場合のみ。
この時の選び方は、Y組の5人から4人を選ぶということなので、
5C4=(5×4×3×1)/(4×3×2×1)=5通り
全体の場合の数は、10人から4人選ぶ組み合わせなので、
10C4=(10×9×8×7)/(4×3×2×1)=210通り
したがって、
210-5=205通り
りんご3個、みかん3個、かき2個がある。 ただし、りんご、みかん、かきの中で区別はないものとする。 ここから4個を取り出したい。 選び方は何通りあるか。
同じものを含むので、場合分けして解く。
・3個が同じ場合
- (りんご・りんご・りんご、みかん)
- (りんご・りんご・りんご、かき)
- (みかん・みかん・みかん、りんご)
- (みかん・みかん・みかん、かき)
の4通り
・2個が同じ場合
- (りんご・りんご、みかん・みかん)
- (りんご・りんご、かき・かき)
- (みかん・みかん、かき・かき)
- (りんご・りんご、みかん、かき)
- (みかん・みかん、りんご、かき)
- (かき・かき、りんご、みかん)
の6通り
したがって、
4+6=10通り
とあるサークルに女性が5人、男性が6人いる。 【1】女性が1人・男性が2人の組み合わせになるように3人を選びたい。選び方は何通りあるか。
【2】女性が2人以上含まれるように5人を選びたい。選び方は何通りあるか。
【3】男女のペアを2ペア作りたい。選び方は何通りあるか。
【1】75通り
5人の女性から1人を選ぶ選び方は「5通り」、6人の男性から2人を選ぶ選び方は「6C2=1通り」となる。
よって「5×15=75通り」となる。
【2】381通り
11人から5人を選ぶ選び方は
「11C5=(11×10×9×8×7)÷(5×4×3×2×1)=55,440÷120=462」となる。そのうち、女性1人、
男性4人を選ぶ選び方は「5C1×6C4=75」、女性0人、男性5人を選ぶ選び方は「6C5=6」と
なる。よって、女性が2人以上含まれるように5人を選ぶ選び方は「462-75-6=381通り」とな
る。
【3】300通り
男女2ペアずつ作るということは、女性から2人・男性から2人を選ぶことと同義である。その
ため、女性は「5C2=10」、男性は「6C2=15」となる。女性2人と男性2人の組み合わせは2
通りとなるため、「10×15×2=300通り」となる。
非言語④:割合と比
ある日の美術館Aの来場者は6000人で、そのうち40%が女性、60%が男性であった。 また、男性の来場者のうち、70%が20歳以上であった。 男性の来場者のうち、20歳未満の人数は何人か。
A:880人
B:980人
C:1080人
D:1180人
E:1280人
F:1380人
G:1480人
H:1580人
問題文を読みながら、順番に人数を計算していきましょう。
全体の来場者数6000人のうち、男性の割合が60%なので、
男性の来場者数は 6000 × 0.60 = 3600 人 です。
このうち、20歳未満の割合は30%であるので、
男性来場者のうち、20歳未満の人数は、
3600 × 0.30 = 1080人
となります。
ある日の美術館Aの来場者は6000人で、そのうち40%が女性、60%が男性であった。 男性の来場者数は変わらず、女性の来場数が1000人増えた。 このとき、女性の来場者数は、全体の何%か。 答えは、小数第1位を四捨五入して求めてください。
A:45%
B:46%
C:47%
D:48%
E:49%
F:50%
G:51%
H:52%
増える前の女性の人数は、6000人の来場者のうち、40%なので、
6000 × 0.40 = 2400 人
です。
女性の人数が、1000人増えるので、
全体の来場者数は、6000 + 1000 = 7000人
女性の来場者数は、2400 + 1000 = 3400人
です。
よって、全体の来場者数に対する女性来場者の割合は、
3400 / 7000 = 48.6 → 49%
赤、青、黄、緑の4色のクレヨンで画用紙を塗りつぶしたい。 画用紙の全体の20%を赤色で塗りつぶした。 残った30%を青色に塗りつぶし、さらに残った部分を黄と緑で4 : 3の割合で塗りつぶした。 この時、黄色のクレヨンで塗りつぶした面積は画用紙全体の何%か。
A:30 %
B:32 %
C:34 %
D:36 %
E:38 %
F:40 %
G:42 %
H:44 %
画用紙の全体の面積を100とします。
赤いクレヨンで塗りつぶした面積は、 100 × 0.20 = 20なので、
残りの面積は、100 – 20 = 80 です。
このうち30%を青いクレヨンで塗りつぶしたので、80 × 0.30 = 24なので、
残りの面積は、80 – 24 = 56 です。
このうち黄:緑 = 4 : 3で塗りつぶすので、黄色のクレヨンで塗る面積は
56 × 4 / 7 = 32%です。
水槽Pの中には、金魚、メダカ、グッピーの3種類の魚がそれぞれ30%、50%、20%の数の割合で入っている。 水槽Qの中には、金魚、メダカ、グッピーの数がそれぞれ20%、40%、40%の割合で入っている。 (1) 水槽Qの魚を全て水槽Pに移した場合、メダカとグッピーの数の比が4:3になった。 最初に水槽Qに入っていた魚の数は、最初に水槽Pに入っていた魚の数の何倍か。
A:1/2 倍
B:7/4 倍
C:3/4 倍
D:3/5 倍
E:3/2 倍
F:7/4 倍
G:2 倍
H:6/5 倍
最初に水槽Qに入っていた魚の数は、最初に水槽Pに入っていた魚の数のX倍とおく。
最初の水槽Pの魚の数を100匹とおくと、水槽Qに入っていた魚の数は100X匹と表せる。
水槽Pの魚の数は、それぞれ(金魚, メダカ, グッピー) = (30, 50, 20) 匹です。
水槽Qの魚の数は、それぞれ(金魚, メダカ, グッピー) = (20X, 40X, 40X) 匹です。
水槽Qの魚を水槽Pに移した後の魚の数は
(メダカ, グッピー) = (50 + 40X, 20 + 40X)
となります。
メダカ:グッピー = 4:3なので、
4:3 = 50 + 40X :20 + 40X
4:3 = 5 + 4X : 2 + 4X
3 (5 + 4X) = 4 (2+4X)
15 + 12X = 8 + 16X
4X = 7
X = 7 / 4
となります。
水槽Pの中には、金魚、メダカ、グッピーの3種類の魚がそれぞれ30%、50%、20%の数の割合で入っている。 水槽Qの中には、金魚、メダカ、グッピーの数がそれぞれ20%、40%、40%の割合で入っている。 水槽Qの魚を全て水槽Pに移した場合、メダカとグッピーの数の比が4:3になった。 その後、水槽Pから金魚を4匹取り出したところ、金魚とグッピーの数が1:2になった。 最初に水槽Qに入っていた魚の数は、何匹か。
A:31匹
B:32匹
C:33匹
D:34匹
E:35匹
F:36匹
G:37匹
H:38匹
最初に水槽Qに入っていた魚の数を100Yとおく。
前の問題より、水槽Pの魚の数は、水槽Qの4/7倍より、100Y× 4/7である。
よって、最初のそれぞれの魚の数は、
水槽P (金魚, メダカ, グッピー) = (30 × 4Y/7, 50 × 4Y/7, 20 × 4Y/7)
水槽Q (金魚, メダカ, グッピー) = (20Y, 40Y, 40Y)
となります。
水槽Pと水槽Qの魚を合わせた後に、金魚を4匹取り出すと、金魚:グッピー = 1:2になるので、
金魚の合計 = (30 × 4Y/7) + (20Y) – 4 = 260Y/7 – 4
グッピーの合計 = (20 × 4Y/7) + (40Y) = 360Y/7
よって、
260Y/7 – 4:360Y/7 = 1 : 2
260Y – 28 : 360Y = 1 : 2
360Y = 2 ( 260Y – 28)
180Y = 260Y – 28
80Y = 28
Y = 28/80 = 7 / 20
よって、水槽Qの魚の数は 100 × 7 / 20 = 35 匹
非言語⑤:損益算
A商店では、4割引で商品を販売したとしても120円の利益が出るように定価設定をしている。 定価1,200円の商品を定価のまま販売した場合、利益はいくらになるか? 解答/解説 600円 定価1,200円の商品の4割引の値段は「1,200×(1-0.4)=1,200×0.6=720円」となる。4割引 ある店では、定価の3割引で売ると400円の利益が得られるように定価設定をしている。 定価の1割引で売った時の利益が940円だったとするとこの商品の定価はいくらか。 定価の3割引と1割引とでは、割引率が「定価の2割分」違う。 つまり、2つの利益の差分が「定価の2割」に相当するということ。 (「利益の差額=定価の2割の金額」) 利益の差額は、 940-400=540円 つまり、定価の2割が540円ということになる。 よって、定価をXとすると X×0.2=540 X=540÷0.2 X=2700円 ある店では、定価の1割引で売っても原価の2割の利益が出るように定価を設定している。 定価が600円の品物の定価はいくらか 定価600円の1割引きである「売値」を求めてから、原価を求めてから原価を求める 「定価×(1-割引率)=売値」なので、 600×(1-0.1)=600×0.9=540円 原価Xの2割の利益が出る売値が540円 原価×(1+利益率)=売値 X×(1+0.2)=540 X=540÷1.2=450円 ある店では、定価の3割引で販売した時に200円の利益が出るように定価を設定をしている。 600円の定価で品物Pを売ると利益はいくらか。 定価600円で売ると、定価の3割+200円の利益が出るので、 600×0.3+200 =180+200 =380円 【別解】 定価600円の3割引の売値は、 売値=600×(1-0.3)=600×0.7=420円 420円の売値のとき、200円の利益が出るので、原価(仕入れ値)は、 原価=420-200=220円 原価220円の品物を定価の600円で売るので、利益は、 利益=600-220=380円 売値が100円の商品Pの仕入れ値が15%上がったために、利益が1割減った。 元の仕入れ値はいくらだったか。 元の仕入れ値をX円とすると、元の利益は、(100-X)円。 15%上がった仕入れ値は1.15円で、その時の利益は、(100-1.15X)円。 これが元の利益から1割減なので、 100-1.15X=(100-X)×0.9 100-1.15X=90-0.9X -1.15X+0.9X=90-100 -0.25X=-10 25X=1000 X=40円 空欄に当てはまる数値を求めなさい。 ある品物に仕入れ値の30%増しの低下をつけたが、セール期間中は割引価格で売ったところ、仕入れ値の4%の利益が得られた。 セール期間中は定価の[ ]%引きで売ったことになる。 (必要な場合は、最後に小数点以下第1位を四捨五入すること)。 まずは、情報を整理する 定価は「仕入れ値の30%増し」なので、「仕入れ値の130%」。 セール期間中の価格は、「仕入れ値の104%」。 仕入れ値をXとすると セール期間中に、定価の何割の価格で売ったのかを「セール期間中の価格÷定価」で求めると 1.04X÷1.3X=1.04÷1.3 =0.8 =80% セール期間中に定価の80%で売ったのだから、 割引は20%。 とある水族館の入館料は、大人が3,200円、子供は大人の3/4の料金である。 また、10名以上の団体で入館する場合は団体割引が適応され、大人は通常料金から25%引き、子供は50%引きとなる。さらに土日は大人・子供ともに追加で10%割引きされる。 【1】土曜日に大人6人・子供8人の団体で入館した場合、入館料の合計はいくらになるか? 【1】21,600円 ◆大人 【2】大人5人・子供7人 ある仕事をPさんが1人ですると12日かかります。 同じ仕事をQさんが1人ですると6日かかります。 2人でこの仕事をすると、何日で終わらせることができるでしょうか。 全体の仕事を1とおくと、 Pさんが1日でする仕事量は、1 / 12 Qさんが1日でする仕事量は、1 / 6 となります。 2人で仕事を終わらせるのにかかる日数をX日とおくと、 PさんがX日でする仕事量は、X / 12 QさんがX日でする仕事量は、X / 6 と表せます。 よって、2人がX日間でする仕事量は、(X / 12) + (X / 6) と表せます。全体の仕事量は1なので、 (X / 12) + (X / 6) = 1 (X / 12) + (2X / 12) = 3X / 12 = X / 4 = 1 X = 4 ある仕事を仕上げるのに、Aさんは12日、Bさんは8日かかる。 また、Aさん、Bさん、Cさんの3人が一緒にこの仕事をすると4日かかる。 この仕事を仕上げるのに、Cさん1人では何日かかるか。 全体の仕事量を1とおきます。 Aさんが1日でする仕事量は、1 / 12 Bさんが1日でする仕事量は、1 / 8 となります。 よって、AさんとBさんの2人が4日間でする仕事量は、 (1 / 12) × 4 + (1 / 8) × 4 = (1/ 3) + (1 / 2) = (2 / 6) + (3 / 6) = 5 / 6 となります。全体の仕事量が1なので、 1 – (5 / 6) = 1 / 6 が、Cさんが4日でした仕事量になります。 よって、Cさんの1日の仕事量は、 (1 / 6 ) / 4 = 1 / 24 Cさんが1人で仕事を終わらせるには、24日かかります。 ある仕事をするのに男性5人だと6日、女性9人だと5日かかる。 この仕事を男性3人、女性2人ですると何日かかるか。 全体の仕事量を1とおきます。 男性1人が1日でする仕事量は、1 / (5×6) = 1 / 30 女性1人が1日でする仕事量は、1 / (9×5) = 1 / 45 となります。 男性3人が1日でする仕事量は、(1 / 30 ) × 3= 1 / 10 女性3人が1日でする仕事量は、(1 / 45 ) × 3= 1 / 15 となります。 よって、男性3人と女性3人が1日でする仕事量は、 (1 / 10) + (1 / 15) = (3 / 30) + (2 / 30) = 5 / 30 = 1 / 6 となります。 よって、仕事を終わらせるのにかかる日数は、6日となります。 ある水槽を満水にするのにP菅だと28分、Q菅だと21分かかります。 この水槽にP菅とQ菅の2つで給水すると、最初に給水を始めてから何分で満水になりますか。 P菅が1分間に給水できる水量は、1 / 28 Q菅が1分間に給水できる水量は、1 / 21 となります。よって、P菅とQ菅の2つで1分間に給水できる水量は、 (1 / 28) + (1 / 21) = (3 / 3×4×7) + ( 4 / 3×4×7) = 7 / 3×4×7 = 1 / 12 したがって、水槽を満水にするためには12分かかります。 ある水槽を満水にするのにP菅だと10分、Q菅だと15分かかります。 また、この水槽が満水のときR管で水を抜くと5分で水槽が空になります。 水槽が満水の時に、P菅とQ菅で給水しながら、R菅で水を抜くと、何分後に水槽は空になりますか。 P菅が1分間に給水できる水量は、1 / 10 Q菅が1分間に給水できる水量は、1 / 15 R菅が1分間に排水する水量は、1 / 5 よって、1分間の水の変化量は、 (1 / 10) + (1 / 15) – (1 / 5) = (3 / 30) + ( 2 / 30) – (6 / 30) = – 1 / 30 となるので、1 / 30 で水量が減ります。 したがって、満水の状態から空になるまでに30分かかります。 Aさん・Bさん・Cさんの3人でレンタカーを借りてドライブに行った。ドライブでかかった費 BさんがAさんに3,300円、CさんがAさんに5,400円ずつ支払えばよい。 ドライブでかかった費用の総額は「15,000+3,900=18,900円」である。18,900円を3人で同じ金額ずつ支払うには、「18,900÷3=6,300」の式から1人6,300円ずつ支払えばよいということになる。 つまり、3人の支払う金額は以下のようになる。 【Aさん:15,000円】 SPIの「速度算」は、平均速度や追い越し・追いつきにかかる時間を求める問題ですが、少しひねった癖のある問題が多いです。 求めるものが時速か分速か、km単位かm単位かといった部分も急いで解くと混乱しがちなので、すばやく慎重に、かつ正確に解く練習として、ここで慣れておきましょう! ではまず問題を解くまえに、SPI非言語の「速度算」を解く際に意識しておいた方が良いポイントや、思考法をまとめておくので参考にしてください! では実際に問題を解いてみましょう! 1周2.7kmの公園の周りをAさんは時速4.8km、Bさんは時速6kmの速度で歩く。現在、AさんとBさんは同じ場所にいる。 【1】14時になったタイミングで2人が反対周りに歩きだすと、2人が再び会うのは何時になるか? 【1】14時15分2人の歩く速度を時速から分速に変換すると、Aさんは80m、Bさんは100mとなる。 つまり、「2700mを分速180m歩く場合にかかる時間」を求めれば良いと言い換えることができる。「 つまり、BさんがAさんに追いつく時間を求めるには、「当初ついていた距離÷1分間で縮まる距離」という式に数字をあてはめればよいため、「240÷20=12」となり、BさんがAさんに追いつくのは14時の3分後に12分を加えた14時15分となる。 甲は2.7km/時で、乙は3.6km/時で歩くものとする。 甲がX地点からY地点まで歩いて42分かかるとき、次の問いに答えなさい。 (2)甲がX地点から歩き始めた5分後に、乙が甲を追ってX地点を出発した。 乙は何分後に追いつくか。 追いつく時間を求める問題です。 「2人の速度の差」の速度で近づいていくのでまずはこの値を求めましょう。 速度の差=3.6-2.7=0.9km/時 甲は5分(5/60時間=1/12時間)で2.7×1/12=0.9/4km進んでいます。 この差を0.9km/時で埋めるので、0.9/4÷0.9=1/4時間=15分となります。 とある小学校の全校生徒300人にアンケートを取ったところ、サッカーが好きな生徒は120人、野球が好きな生徒は80人、バスケットボールが好きな生徒は60人いた。 【1】サッカーと野球の両方が好きな生徒が35人いた。サッカーと野球のいずれか片方だけを好きな生徒は何人いるか? 【1】130人 6本のくじがあります。 このうち2本が当たり、残りの4本がハズレです。 このくじから2本同時に引くとき、1本だけ当たる確率はいくらか。 (解法1) 組み合わせを考える 6本のくじから同時に2本を引くとき、取り出し方の組み合わせは、6C2 = 15 2本の当たりのうち、1本を取り出す組み合わせは、2C1 = 2 4本のハズレから、1本を取り出す組み合わせは、4C1 = 4 よって、2 × 4 / 15 = 8 / 15 (解法2) 1本ずつ確率を考える 同時に2本取り出したとありますが、1本目を選んで、その後に2本目を選んでから結果を見る場合も同じです。 そのため、1本ずつ順番に選んだと考えることもできます。 2本のうち、1本だけ当たりを引く場合は、 ・1本目に当たりを引き、2本目にハズレを引く場合 2 / 6 × 4 / 5 = 8 / 30 ・1本目にハズレを引き、2本目に当たりを引く場合 4/ 6 × 2/ 5 = 8 / 30 の2通りがあります。 これらは、同時に起こらないため、和を求めて、 8 / 30 + 8 / 30 = 8 / 15 となります。 ある少年Aが、けん玉をする。 玉が剣に刺さる確率は、1回目が0.5、2回目が0.7であることがわかっている。 この時、2回とも玉が剣に刺さる確率はいくらか。 繰り返し行う事象の場合、1回ごとの確率をかけることで、同時に起こる確率を計算することができます。 「1回目に玉が剣に刺さる確率」×「2回目に玉が剣に刺さる確率」 = 0.5 × 0.7 = 0.35 となります。 ある少年Aが、けん玉をする。 玉が剣に刺さる確率は、1回目が0.5、2回目が0.7であることがわかっている。 この時、2回のうち1回だけ玉が剣に刺さる確率はいくらか。 2回のうち1回だけ玉が剣に刺さる事象は、 ①「1回目に玉が剣に刺さる」かつ「2回目に失敗する」 ②「1回目に失敗する」かつ「2回目に玉が剣に刺さる」 の2つの場合が考えられます。 ①②は同時に成立しないので、これぞれの確率を足し合わせることで計算することができます。 ①の確率:0.5 × 0.3 = 0.15 ②の確率:0.5 × 0.7 = 0.35 よって、0.15 + 0.35 = 0.50 となります。 大小2つのサイコロがあります。 これらの2つサイコロを同時に1回投げて、その和が10になる確率はいくらですか。 1つのサイコロの目の出方は6通りあるので、2つのサイコロの目の組み合わせは 6 × 6 = 36 通り です。 大小2つのサイコロの目の和が10になる組み合わせは、 (大, 小) = (4, 6)、(5, 5)、(6, 4) の3通りあります。 よって、求める確率は、3/36 = 1/12 となります。 大小2つのサイコロがあります。 これらの2つのサイコロを同時に1回投げて、その積が偶数になる確率はいくらですか。 2つの数字の積が偶数となる場合を考えます。 ①:偶数 × 偶数 = 偶数 ②:偶数 × 奇数 = 偶数 ③:奇数 × 偶数 = 偶数 ④:奇数 × 奇数 = 奇数 よって、①②③のように少なくとも一方が偶数の目が出れば良いことが分かります。 ①②③の確率をそれぞれ計算して和を求めても良いですが、計算量が少なくなるように工夫しましょう。 (積が偶数になる確率) + (積が奇数になる確率) = 1 より (積が偶数になる確率) = 1 – (積が奇数になる確率) となるので、積が奇数となる確率④の確率を求めて1から引くことで計算すると、計算が少なく済みそうです。 サイコロの目のうち、奇数の目は(1, 3, 5)の3通りなので、 大小がともに奇数となるのは、3 × 3 = 9 通りです。 よって、積が奇数になる確率は、9 / 36 = 1 / 4 であり、 積が偶数になる確率は、1 – 1 / 4 = 3 / 4 となります。 箱の中に赤い紙が2枚、青い紙が3枚、黄色の紙が4枚入っている。この箱の中から3枚の紙を取り出す。(一度取り出した紙は箱の中には戻さない) 【1】赤い紙→青い紙→黄色の紙の順番で取り出す確率は? 【1】1/21 とある会社の新卒研修にて、210名の新卒が3人グループ・4人グループ・5人グループに分類され、計50個のグループができた。 【1】4人グループが30個あった場合、5人グループは何個あるか? 【1】15個 薬品PとQを1:3で混ぜた混合液Xと、2:3で混ぜた混合液Yを同量混ぜて薬品Rを作った。Rに含まれるPの割合はどれだけか。 混合液X・・・P:Q=1:3なので、X全体を4とするとPは1/4 混合液Y・・・P:Q=2:3なので、Y全体を5とするとPは2/5 RはXとYを同量混ぜているので、Rに含まれるPの割合は、 (1/4+2/5)÷2=13/20÷2=13/40=0.325 【正解】32.5% 赤ワインPと白ワインQを2:3で混ぜたロゼワインXと、赤ワインPと白ワインRを3:7で混ぜたロゼワインYがある。 ロゼワインXとロゼワインYを2:1で混ぜて、ロゼワインZを作った。 Zに含まれる赤ワインPの割合はどれだけか。 XとYを2:1で混ぜるので、全体量を30とすると、Xは20になる。 その中では、P:Q=2:3=8:12。 Yは10で、その中では、P:R=3:7。 全体量30の中で、Pは8+3=11を占めるので、 11÷30=0.366・・・→37% 【解答】37% 赤ワインPと白ワインQを2:3で混ぜたロゼワインXと、赤ワインPと白ワインRを3:7で混ぜたロゼワインYがある。 ロゼワインXとロゼワインYを2:1で混ぜて、ロゼワインZを作った。 ロゼワインZの試飲を7人で行うので、用意したワインを7等分したが、直前で1人が欠席になったため、ワインを6等分した。 6等分した量は7等分した量より1杯あたり20cc多くなった。 用意したワインの量はどれだけか。 1/6と1/7の差は、 1/6-1/7=(7-6)/42=1/42 20cc=1/42なので、全体は、 20÷1/42=20×42=840cc 【解答】840cc ある人が車を購入した。 購入時に総額の1 / 5を支払い、残額を12回に均等に分割して支払う。 分割払いの1回当たりの支払額は総額のどれだけにあたるか。 ただし、手数料はかからないものとする。 購入時に、総額の1 / 5を払っているため、 1 – (1 / 5) = 4 / 5 より、残額は総額の4 / 5です。 残額を12回に分割して支払うため、 ( 4 / 5 ) × ( 1 / 12 ) = (1 / 5) × (1 / 3) = 1 / 15 より、分割払い1回あたりの支払額は 1/ 15となります。 パソコンを9回の分割払い購入した。 購入時に代金総額の1 / 5を支払い、2回目以降は均等に支払うこととした。 この時、2回目の支払額は、総額のどれだけに当たるか? ただし、利子はかからないものとする。 この問題は、順番に残額を確認することがポイントです。 初回は、総額の1 / 5を支払うので、 1 – (1 / 5) = 4 / 5 より 残高は総額の4 / 5 です。 総額の4 / 5を残り8回で均等に支払うので、2回目以降の支払い額は、 (4 / 5) x (1 / 8) = (1 / 5) x (1 / 2) = 1 / 10 より、 2回目の支払い額は、総額の 1 / 10となります。 新しく液晶テレビを購入し、代金は3回に分けて支払うことにした。 初回は総額の3 / 8を支払った。 2回目に初回の2 / 3を支払い、3回目に残額を全て支払うとき、3回目に支払う金額は初回のどれだけに当たるか。 ただし、利子はかからないものとする。 先ほどの問題と違い、初回に対してどれくらいか、を聞かれていることに注意しましょう。 この問題は、まず3回目に支払う金額が、総額の何割かを出す必要があります。 初回は、問題文から総額の1 / 4を支払っています。 2回目は、初回の2 / 3を支払うので、 (1 / 4) x (2 / 3) = 1 / 6 となります。 2回目までの支払い額は、初回と2回目の支払いの合計なので、 (1 / 4) + (1 / 6)= (3 / 12) + (2 / 12) = 5 / 12 です。 この残りを3回目で全て支払うため、3回目の総額に対する支払い額は、 1 – (5 / 12) = 7 / 12 となります。 今回聞かれているのは、初回の支払い額に対する3回目の支払い額なので、 (7 / 12) / (1 / 4) = (7 / 12) x (4 / 1) = 7 / 3 となります。 ある人が、エアコンを分割払いで購入することにした。 購入時に価格の何割かを頭金を支払い、 総額から頭金を差し引いた残額を4回に分割して支払う。 このとき、分割手数料として残額の1 / 5を加えた額を4等分して支払うこととなる。 頭金が購入価格の1 / 6 のとき、分割払い1回あたりの支払い額は購入価格のどれだけにあたるか。 まず、利子を含めた、残高を計算します。 頭金が購入価格の1 / 6なので、元の残高は、5 / 6です。 この残高に利子として、残高の1 / 5が加えられるため、 (5 / 6) + ( (5 / 6) × (1 / 5) ) = (5 / 6) + (1 / 6) = 1 が、分割前の金額になります。 これを、4等分して支払うため、 1 × (1 / 4) = 1 / 4 が答えです。 ある人が、新しくカメラを分割払いで購入することとした。 購入時に価格の何割かを頭金として支払い、 総額から頭金を差し引いた残額を8回に均等に分割して支払うことにした。 このとき、分割手数料として残額の1 / 5を加えた額を8等分して支払うこととなる。 分割払い1回の支払い額を購入価格の1 /10にするためには、頭金として購入価格のどれだけを支払えばよいか。 頭金をxとおくと、 元の残高は、( 1 – x )であり、利子として、残高の1 / 5が加えられるため、 ( 1 – x ) +( 1 – x ) × (1 / 5) = (1 – x) × (6 / 5) となります。 この、利子を含めた残高を8回で支払ったとき、1回の支払い額が購入価格の1 /10となるため、 ( 1 – x ) × ( 6 / 5 ) × (1 / 8) = 1 / 10 これをxについて解くと x = 1 / 3 となり、答えは 1 / 3となります。 赤ワインPと白ワインQを2:3で混ぜたロゼワインXと、赤ワインPと白ワインRを3:7で混ぜたロゼワインYがある。 ロゼワインXとロゼワインYを2:1で混ぜて、ロゼワインZを作った。 ロゼワインZの試飲を7人で行うので、用意したワインを7等分したが、直前で1人が欠席になったため、ワインを6等分した。 6等分した量は7等分した量より1杯あたり20cc多くなった。 用意したワインの量はどれだけか。 1/6と1/7の差は、 1/6-1/7=(7-6)/42=1/42 20cc=1/42なので、全体は、 20÷1/42=20×42=840cc 【解答】840cc P、Q、R、Sの4人が1冊の本を順番に読んだ。 4人の読んだ順番について、次のことがわかっている。 (1)次の推論ア、イ、ウのうち、必ずしも誤りとは言えないものはどれか。 AからHまでの中から1つ選びなさい。 【選択肢】 A:アだけ E:アとウの両方 Ⅰ.から、読んだ順番は、 SP〇〇、〇SP〇、〇〇SP の3通りが考えられます。 これにⅡ.の情報を加えると、 SPQR、QRPR、QRSP、SPRQ の4通りが考えられます。 これと推論を比較すると、 ア:先の4通りに、該当するものがない イ:SPRQが該当する ウ:該当するものがない したがって、「必ずしも誤りとは言えない」のはイだけです。 よって、Bとなります。 では続きの問題もやってみましょう↓ P、Q、R、Sの4人が1冊の本を順番に読んだ。 4人の読んだ順番について、次のことがわかっている。 (2)最も少ない情報で4人の読んだ順番が全てわかるためには、ⅠとⅡのほかに、次のカ、キ、クのうちどれが加われば良いか。 AからHまでの中から1つ選びなさい。 【選択肢】 A:カだけ E:カとクの両方 SPIは今回のように大問1つに対して2つ以上小問が出題されることがよくあります。 このような場合は前回の「問題1」で出した答えをうまく利用して答えを出すことが最速解答へつながります! すでに(1)で、可能性のある順番は次の4通りとわかっています。 カ:左からP、Qの順に並んでいるのは、1と2 キ:左からR、Qの順に並んでいるのは、2だけ ク:左からS、Rの順に並んでいるのは、aとbとc したがって、キの情報が加われば、1通りに絞ることができます。 新しく液晶テレビを購入し、代金は3回に分けて支払うことにした。 初回は総額の3 / 8を支払った。 2回目に初回の2 / 3を支払い、3回目に残額を全て支払うとき、3回目に支払う金額は初回のどれだけに当たるか。 ただし、利子はかからないものとする。 先ほどの問題と違い、初回に対してどれくらいか、を聞かれていることに注意しましょう。 この問題は、まず3回目に支払う金額が、総額の何割かを出す必要があります。 初回は、問題文から総額の1 / 4を支払っています。 2回目は、初回の2 / 3を支払うので、 (1 / 4) x (2 / 3) = 1 / 6 となります。 2回目までの支払い額は、初回と2回目の支払いの合計なので、 (1 / 4) + (1 / 6)= (3 / 12) + (2 / 12) = 5 / 12 です。 この残りを3回目で全て支払うため、3回目の総額に対する支払い額は、 1 – (5 / 12) = 7 / 12 となります。 今回聞かれているのは、初回の支払い額に対する3回目の支払い額なので、 (7 / 12) / (1 / 4) = (7 / 12) x (4 / 1) = 7 / 3 となります。 ある人が、エアコンを分割払いで購入することにした。 購入時に価格の何割かを頭金を支払い、 総額から頭金を差し引いた残額を4回に分割して支払う。 このとき、分割手数料として残額の1 / 5を加えた額を4等分して支払うこととなる。 頭金が購入価格の1 / 6 のとき、分割払い1回あたりの支払い額は購入価格のどれだけにあたるか。 まず、利子を含めた、残高を計算します。 頭金が購入価格の1 / 6なので、元の残高は、5 / 6です。 この残高に利子として、残高の1 / 5が加えられるため、 (5 / 6) + ( (5 / 6) × (1 / 5) ) = (5 / 6) + (1 / 6) = 1 が、分割前の金額になります。 これを、4等分して支払うため、 1 × (1 / 4) = 1 / 4 が答えです。 ある人が、新しくカメラを分割払いで購入することとした。 購入時に価格の何割かを頭金として支払い、 総額から頭金を差し引いた残額を8回に均等に分割して支払うことにした。 このとき、分割手数料として残額の1 / 5を加えた額を8等分して支払うこととなる。 分割払い1回の支払い額を購入価格の1 /10にするためには、頭金として購入価格のどれだけを支払えばよいか。 頭金をxとおくと、 元の残高は、( 1 – x )であり、利子として、残高の1 / 5が加えられるため、 ( 1 – x ) +( 1 – x ) × (1 / 5) = (1 – x) × (6 / 5) となります。 この、利子を含めた残高を8回で支払ったとき、1回の支払い額が購入価格の1 /10となるため、 ( 1 – x ) × ( 6 / 5 ) × (1 / 8) = 1 / 10 これをxについて解くと x = 1 / 3 となり、答えは 1 / 3となります。 赤ワインPと白ワインQを2:3で混ぜたロゼワインXと、赤ワインPと白ワインRを3:7で混ぜたロゼワインYがある。 ロゼワインXとロゼワインYを2:1で混ぜて、ロゼワインZを作った。 ロゼワインZの試飲を7人で行うので、用意したワインを7等分したが、直前で1人が欠席になったため、ワインを6等分した。 6等分した量は7等分した量より1杯あたり20cc多くなった。 用意したワインの量はどれだけか。 1/6と1/7の差は、 1/6-1/7=(7-6)/42=1/42 20cc=1/42なので、全体は、 20÷1/42=20×42=840cc 【解答】840cc 【問題】設問で示された二語の関係を考えて、それと対応する関係となるように( )に当てはまる語句を選びなさい。 ❶ A:切る ❷ A:元号 ❸ A:辺境 C(文房具) 大学は、教育機関の一種なので、包含関係が成立しています。 B(慶応) 社会は、理科と同様に科目であるため、並列関係が成立しています。 A(辺境) 強調は、隠蔽と逆の意味であるため、対義語関係が成立しています。 【問題】設問で示された二語の関係を考えて、対応する関係となるものを選びなさい。 ❶ 心配:懸念 ア 学校:組織 ❷ タピオカ:キャッサバ ア 日本酒:米 ❸ 維持:現状 ア 学校:卒業 イ(故人:死者) 心配と懸念は、同義語の関係にあります。 ア(日本酒:米) タピオカの原料は、キャッサバなので原料関係が成立します。 ウ(緩和:規制) 「維持」の目的語は「現状」となるので、動詞と目的語関係が成立しています。 例題:提示された二語の関係を考え、同じ関係のものを選びなさい。 A:アだけ D:アとイ 正解:A 正解:2 「我田引水」:自分の好きなように図って、他人の都合は考えないこと。 自分の都合だけを考えること。 また、そのさま。 てまえがって。 下線部の言葉と意味が合致するものを、AからEの中から一つ選びなさい。 いみじくも A 適切に 正解:A 音信:たより。おとずれ。手紙。おんしん。 着信:電報・(携帯)電話・郵便などの通信が到着すること。 連絡:別々のものの間のつながりあい。「―を取る(=つける)」。つながりがつくこと。「このバスは急行列車に―する」。つながりをつけること。 報告:告げ知らせる、特に、任務・調査などを行った情況や結果について述べること。また、その内容。 消息:たより。手紙。知らせ。 「たより、知らせ」という意味は「音信」と「消息」に共通しているので、「4」の消息が正解です。 例題:下線部の語が最も近い意味でつかわれているものを、AからEの中から一つ選びなさい。 電車でいく A 熱で休む 正解:E 次に示された文章の下線部の意味を考え、最も近い意味で使われているものを選択肢より1つ選びなさい。 ・例題) 母より手紙が届いた。 例題の「より」は、作用の起点を表す核助詞であり「母から」に置き換えられます。 A. 比較を表す格助詞の「より」で「〜よりも」に置き換えられます。 B. 比較を表す格助詞の「より」で「〜よりも」に置き換えられます。 C. 「〜により」で、格助詞「に」+動詞「よる」です。「〜によって」に置き換えられます。 D. 車道寄りです。 AからEの語句を空欄〔1〕から〔5〕に入れて意味が通る文を完成させたとき、〔4〕に当てはまるのは次のうちどれか。 カシやナラで作る白炭は〔1〕〔2〕〔3〕〔4〕〔5〕吸収する力もある A 遠赤外線を放射する 正解:B 次のア~オの文を意味が通るように並び換えたとき、イの次にくる文を選びなさい。 ウ→イ→エ→ア→オ の順で並べると意味が通る文章になります。 C. エ 文中の空欄に入る最も適切な表現は次のうちどれか。 特に、山間部では危機的だと言われている。 A 空洞化 正解:A 次の文の空欄( )に入れるのに適切なものはどれか、A~Eの中から1つ選びましょう。 イギリス人の祖先はヨーロッパ大陸からやって来たので、初期のイギリスの法制度は基本的に他のゲルマン諸民族と共通であった。( )、イギリスでは6世紀末からキリスト教の影響により、特に家族法に関して独自の制度が生み出させた。 空所の前後に注目しましょう。 空所の前では、「イギリスの法制度はゲルマン諸民族と共通であった」と述べられています。 空欄の後では、「イギリスの〜家族法に関して独自の制度が生み出された」と述べられています。 したがって、対比関係を表す「しかし」が当てはまります。 次の文章を読んで、設問に答えなさい。 人権と民主主義という理念において、建国以来アメリカほど変わらない国はない。それは本来、近代世界の( i ) な理想だったが、アメリカはどの国より挫折を知らず、一貫してその実現に努めてきた。まさにその点でこの国は青年に似ているのであって、生涯に恥と悔恨の思いでを持っていない。この世に悪があることを認めない国、と『アメリカ病』の著者ミシェル・クロジェ氏は嘆いたが、それはこの国が( ii )に若いということなのである。 若いといえば、アメリカはまた( iii )にも大国でありながら青年期にいる。この十年、日本を筆頭に多くの先進国が消費不況に苦しむ中で、この国だけは旺盛な購買意欲を見せている。膨大な貿易赤字をものともせず、日本からも中国からも最大の輸入国でありつづけている。生活を物質的に豊かにし、それによって社会の階段を登ろうとする点で、アメリカ人はいまも青春の夢を追っている。 考えればこれは奇跡的な話であって、現代文明が大きく転換する過程で、例外的に起こった現象と見るほかない。なぜなら世界がポスト工業社会に入り、商品消費よりサービス消費へと移るなかで、先進国の購買意欲はむしろ落ちるのが当然だからである。日本の現状は極端だとしても、箪笥にものが溢れ、ごみの捨て場に困り、環境と資源枯渇は心配になるのは、文明かくに共通の傾向だろう。 (中略) 評論家で『幻想の超大国』を書いた、デヴィットハルバースタム氏によれば、かつては自動車がステータス・シンボルの代表的な物差しであって、シボレーからキャディラックに至る細かな段階があったという。今日も住宅地には目に見える階層制があって、消費者は出世とともに家を買い替える。先ごろ、テレビが防壁で囲まれた金持ちの団地の様子を伝えていたが、そこに住んで、脱落するまいと努める若い夫婦の姿には涙ぐるましいものがあった。 昔は日本にも「三種の神器」と呼ばれ、国人が争ってかうステータス・シンボルがあった。だがあれはむしろ平等の象徴であり、人は隣と同じになるために同じ商品を買っていたにすぎない。その点、アメリカでは消費も優越のための競争であるから、意欲が衰える飽和状態が来るとは考えにくい。この国の消費の若さは、文化の構造に根ざしているのである。 日本がこのアメリカになれる可能性はないし、またその必要もない。将来の日本は若干の移民を受け入れながら、基本的には老熟した「寡民小国」に落ち着くことになろう。高度の知的産業、文化さ産業、海外投資の収益と対人サービスで経済を支え、省資源、環境保護を誇りとして生きるほかあるまい。 だが文明がこの新しい平行状態に達するには、当然まだ時間がかかる、移行段階を生き延びるには輸出が不可欠であって、そのためにはあの若い隣国の健在を祈るほかない。ドルの行く手に不安は多くとも、当分の間、日本は対米投資を増加するほかないはずである。 (山崎正和「アメリカを問い直す」) 解説 設問(1) ( i )について、空欄前の「それは本来、」は人権と民主主義を指す。近代以降、各国が人権と民主主義を理想にしてきたが、アメリカが1番、理想を実現させてきた、という文脈になります。。(1)には、近代世界が、共通して長く求めてきた理想という意味の言葉が入り、選択肢では「普遍的」が適当です。 ( ii )について、空欄前の「この世に悪があることを認めない国」=「この国が( ii ) に若い」となるように( ii )に言葉を入れればよいことがわかります。善悪に関係がある言葉は、選択肢では「道徳的」が適当です。 ( iii )について、空欄後の「多くの先進国が消費不況に苦しむ中で、この国(=アメリカ)だけは旺盛な購買意欲を見せている」 = 「アメリカはまた( iii ) にも〜青年期にいる」となるように( iii )に言葉を入れればよいことが分かります。選択肢では「経済的」が適当です。 設問(2) 「この国の消費の若さ」とは、消費不況を経験していないアメリカでは、国民の購買意欲が高く、物を買って物質的に豊かになることが社会的な階級の向上のステータスになるという文化を表現した言葉です。選択肢では、イのみが該当します。アとウはともに対比として示されているアメリカ以外の国の状況を表しています。 設問(3) 平行状態とは、釣り合いが取れた安定した状態のことを意味します。「この」とあるので、前の段落に注目すると、「寡民小国に落ち着く」とあるので、これが平行状態にあたります。「寡民=少ない人」ということから、選択肢の「イ:人口減少」が該当します。また、具体例として挙げられている部分と選択肢を比較してみると、「ウ:海外投資」も該当することが分かります。 設問(4) アについて、1段落目に「一貫してその(=人権と民主主義の)実現に努めてきた」とあるので合致します。イについて、本文中で述べられている「若さ」とは「アメリカ文化を表す比喩」として使われているため、「アメリカ人の若いときの夢の実現」は本文とは無関係です。ウについて、アメリカでは消費によって社会的な階級を象徴する文化があることが述べられており、5段落目に「消費も優越のための競争である」とあることから合致します。 例題:以下の熟語の成り立ち方として当てはまるものを、AからEの中から一つ選びなさい。 強弱 A 主語と述語の関係である 正解:D 次の5つの熟語の成り立ち方として、当てはまるものをA~Dの中から1つずつ選びなさい。 絵画 「絵画」のそれぞれの漢字はともに描いたものの意味があり「似た意味を持つ漢字を重ねる」に分類されます。 選択肢にはないので、正解はDの「上記のどれにも当てはまらない」となります。 次の5つの熟語の成り立ち方として、当てはまるものをA~Dの中から1つずつ選びなさい。 仰天 「仰」は「仰ぐ(あおぐ)」と読み、見上げるという動詞の意味があります。 目的語として後ろに「天」が来ており、「天を仰ぐ」となるので、正解はC:動詞の後に目的語をおくになります。 仰天は「空を見上げるほど、ひどく驚く」という意味です。 次の5つの熟語の成り立ち方として、当てはまるものをA~Dの中から1つずつ選びなさい。 日没 「日没」は「日が没む(しずむ)」という成り立ちです。 「日」が主語、「没」が述語の関係なので、正解はB:主語と述語の関係にあるとなります。 次の5つの熟語の成り立ち方として、当てはまるものをA~Dの中から1つずつ選びなさい。 実施 「実施」は、「実際に施す(ほどこす)」となるので、 「実」という副詞が「施」という動詞を修飾しています。 正解は、A:前の感じが後の漢字を修飾するとなります。 次の5つの熟語の成り立ち方として、当てはまるものをA~Dの中から1つずつ選びなさい。 及落 「及落」は「及第(試験に合格すること)」と「落第(試験に落ちること)」と考えると反対の意味であることが分かります。 正解は、C:反対の意味の漢字を重ねるです。 1 瓦解 がかい 組織的な物事の一部分が壊れて、それによって全体がこわれること 1 首尾一貫 しゅびいっかん 考えや態度などが矛盾無く終始する 次の空欄に当てはまるように文節を並び替えたとき、[ 3 ]に当てはまるものはどれでしょうか。 十字軍が勝利した後[ 1 ][ 2 ][ 3 ][ 4 ][ 5 ]にすぎなかった。 B→E→D→C→A と並べると、文章が成立します。 次の文の空欄( )に入れるのに適切なものはどれか、A~Eの中から1つ選びましょう。 イギリス人の祖先はヨーロッパ大陸からやって来たので、初期のイギリスの法制度は基本的に他のゲルマン諸民族と共通であった。( )、イギリスでは6世紀末からキリスト教の影響により、特に家族法に関して独自の制度が生み出させた。 空所の前後に注目しましょう。 空所の前では、「イギリスの法制度はゲルマン諸民族と共通であった」と述べられています。 空欄の後では、「イギリスの〜家族法に関して独自の制度が生み出された」と述べられています。 したがって、対比関係を表す「しかし」が当てはまります。
で商品を販売したとしても120円の利益が出るため、「720-120=600」という計算式から原
価は600円ということが分かる。つまり、定価1,200円の商品を定価のまま販売した場合の
利益は「1,200-600=600」となり、利益は600円ということが分かる。
非言語⑥:料金割引
【2】水曜に大人・子供あわせて12人の団体で入館したところ、入館料の合計は20,400円であった。12人の内訳は大人・子供それぞれ何人か?
団体割引も土日割引も適応されるため、大人・子供それぞれ一人あたりの金額を求める必要がある。
3,200×0.75(3/4)×0.9(9/10)=2,160円
◆子供
3,200×0.75(3/4)×0.5(1/2)×0.9(9/10)=1,080円
大人6人・子供8人の団体であるため、
「2,160×6+1,080×8=12,960+8,640=21,600」となり、入館料の合計は21,600円となる。
水曜日に12人の団体で入館するため、団体割引は適応されるが土日割引は適応されな
い。つまり、一人あたりの入館料は大人2,400円、子供1,200円となる。仮に大人の人数を
X人とした場合、「2400X+1200(12-X)=20400」となる。この式を計算するとX=5となり、大
人の人数は5人ということが分かる。大人の人数が5人ということは子供の人数は「12-5=7
人」となるため、12人の内訳は大人5人・子供7人となる。非言語⑦:仕事算
A:1日
B:2日
C:3日
D:4日
E:5日
F:6日
G:7日
H:8日
A:20日
B:21日
C:22日
A:5日
B:6日
C:7日
D:8日
E:9日
F:10日
G:11日
H:12日
A:9分
B:9分30秒
C:10分
D:10分30秒
E:11分
F:11分30秒
G:12分
H:12分30秒
A:25分
B:26分
C:27分
D:28分
E:29分
F:30分
G:31分
H:32分
非言語⑧:代金精算
用はレンタカー代とガソリン代のみである。レンタカー代の15,000円はAさんがまとめて
支払った。ガソリン代の3,900円は、Bさんが3,000円・Cさんが900円支払った。3人が同
じ金額ずつ支払うように調整するためには、誰が誰に何円ずつ支払えばよいのか?
すでに6,300円以上支払っているため、誰かに支払う必要はない。
【Bさん:3,000円】
6,300-3,000は3,300円となり、Aさんに3,300円支払わなければならない。
【Cさん:900円】
6,300-900は5,400円となり、Aさんに5,400円支払わなければならない。非言語⑨:速度算
「速度算」を解く時の大事なポイント!
【2】14時にAさんが歩き始め、その3分後にBさんが同じ周り方で歩きだした場合、BさんがAさんに追いつくのは何時になるか?
2700÷180=15」であるため、次に2人が会うのは14時の15分後である14時15分となる。
【2】14時15分
上記の【1】で求めた数値を参考にすると、2人の歩く速度は1分間で20mの差がつく。AさんはBさんよりも3分早く歩き始めているため、「80×3=240m」の差がついている。非言語⑩:集合
【2】上記の【1】で取り上げた条件に加え、バスケットボールだけが好きな生徒が25人いた。
サッカー・野球・バスケットボールのいずれも好きではない生徒は何人いるか?
サッカーが好きな生徒の人数・野球が好きな生徒の人数、それぞれから35人を除けば良いため、「(120-35)+(80-35)=85+45=130人」となる。
※「120+80-35=165人」と間違えないように気をつける。
【2】110人
上記の【1】で求めた数値も活用した場合、サッカー・野球・バスケットボールのいずれも好きではない生徒は「全校生徒-(サッカーと野球のいずれか片方だけを好きな生徒+サッカーと野球の両方が好きな生徒+バスケットボールだけが好きな生徒)」で求められる。
この式に数値をあてはめると
「300-(130+35+25)=300-190=110人」となる。非言語11:確率
A:1/5
B:2/5
C:3/10
D:1/15
E:2/15
F:4/15
G:8/15
H:7/30
A:0.12
B:0.20
C:0.35
D:0.40
E:0.50
F:0.63
G:0.70
H:0.80
A:0.12
B:0.20
C:0.35
D:0.40
E:0.50
F:0.63
G:0.70
H:0.80
A:1/2
B:1/3
C:1/4
D:3/4
E:1/12
F:1/36
G:5/12
G:5/36
A:1/2
B:1/3
C:1/4
D:3/4
E:1/12
F:1/36
G:5/12
G:5/36
【2】同時に3枚の紙を取り出す場合、青い紙1枚と黄色の紙2枚を取り出す確率は?
それぞれの色の紙を取り出す確率を求めれば良いため、
「2/9×3/8×4/7=24/504=1/21」となる。
【2】3/14
青い紙1枚と黄色の紙2枚を取り出す組み合わせを全体の組み合わせで割れば良いた
め、「3C1×4C2/9C3=18/84=3/14」となる。非言語12:特殊算
【2】4人グループと5人グループの数が同じだった場合、3人グループは何個あるか?
4人グループが30個あるということは「4×30=120」となり、3人グループ・5人グループのいずれかに分類されるのは「210-120=90」となる。3人グループがX個あったと仮定すると、5人グループは(20-X)個になる。
つまり「3X+5(20-X)=90」の式となり、この式を計算すると
X=5となる。
3人グループは5個あるということは5人グループは15個あるということになる。
【2】10個
4人グループと5人グループの数が同じであり、両方のグループ数をXとした場合、3人グループの数は「50-2X」となる。これらの条件を式にあてはめると「4X+5X+3(50-2X)=210」
となり、計算すると「X=20」となる。4人グループと5人グループはそれぞれ20個あるため、「50-20×2=10」となり、3人グループは10個あることが分かる。非言語13:濃度
非言語14:分割払い
非言語15:順番を答える問題
B:イだけ F:イとウの両方
C:ウだけ G:アとイとウの全て
D:アとイの両方. H:全て間違い
B:キだけ F:キとクの両方
C:クだけ G:カとキとクの全て
D:カとキの両方. H:すべてが加わってもわからな
~第3章~言語
言語①:二語関係
大学:教育機関
ハサミ:( )
B:カッター
C:文房具
D:やすり
社会:理科
大正:( )
B:慶応
C:現代
D:年号
強調:隠蔽
中原:( )
B:郊外
C:上流
D:全体
ハサミと包含関係が成立するのは、Cの文房具になります。
そのため、元号である大正と並列関係が成立するのは、Bの慶応となります。
そのため、中原(ちゅうげん)の対義語に当たる語句は辺境なので答えはAとなります。
イ 故人:死者
ウ 貧富:格差
イ 穀物:麦
ウ ウイスキー:芋
イ 命令:懲戒
ウ 緩和:規制
そのため、故人と死者は同じ意味の同義語関係に当たるため、答えはイになります。
そのため、日本酒と米という原料関係が成立しているアが正解になります。
そのため、緩和と規制という目的語と動詞関係にあるウが答えになります。
人間:哺乳類
ア:鉛筆:文房具
イ:教会:牧師
ウ:日食:月食
B:イだけ E:イとウ
C:ウだけ F:アとウ言語②:熟語
 就活アドバイザー 京香
就活アドバイザー 京香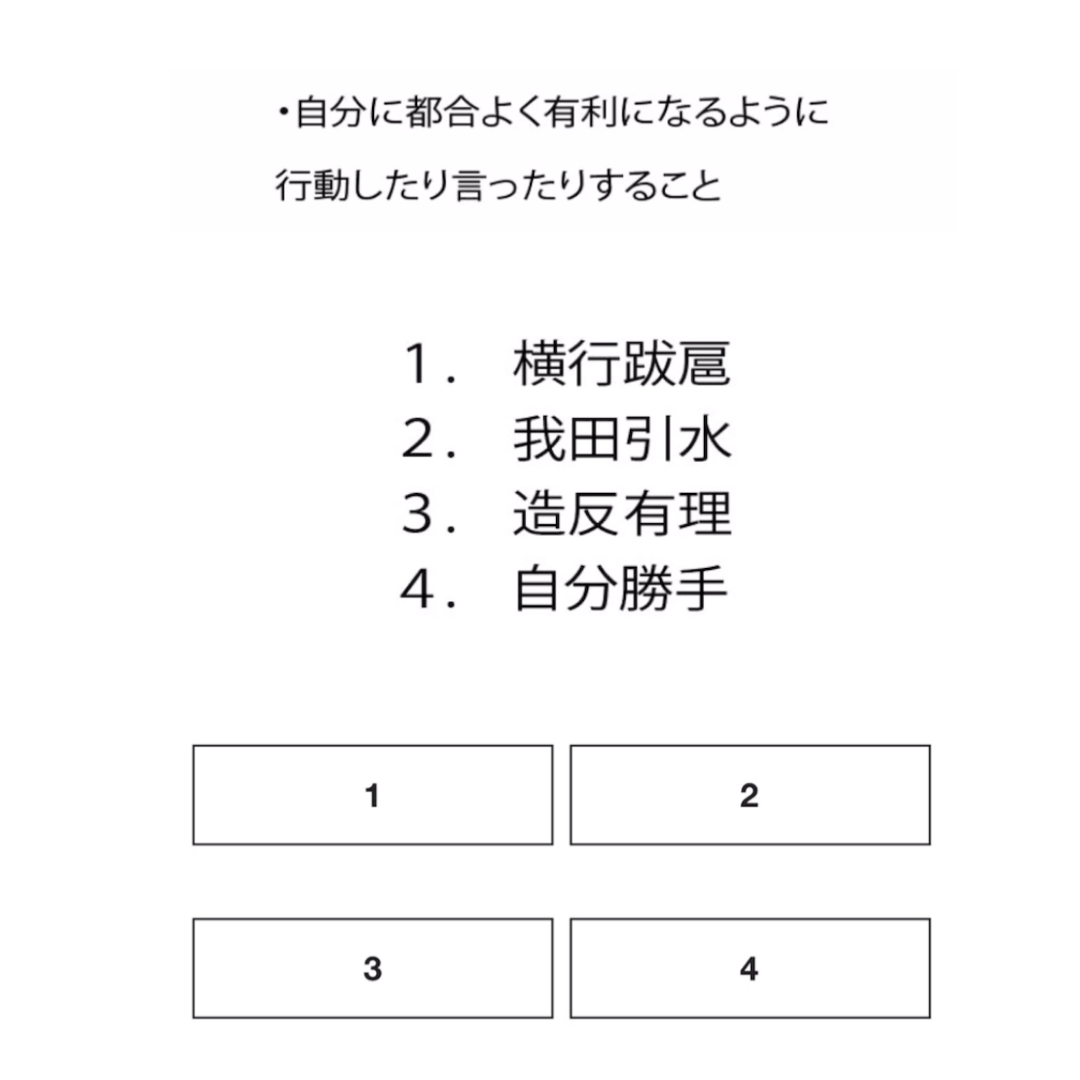
 就活アドバイザー 京香
就活アドバイザー 京香
B はぐらかす
C 大いに
D それでも
E むげに言語③:語句の用法

B コンビニで買う
C 夫婦で暮らす
D 飛んできたもの
E ギターで華を添える
言語④:文の並び替え
B 特性に加えて
C 安定した火力で
D 汚れや臭いを
E 着火が難しいが
A.ア
B.ウ
C.エ
D.オ
E.イが最後の文
言語⑤:空欄補充
若者が都市部に働きに出てしまい、現地で結婚してしまうため帰ってこないのだ。
ここで人口の〔 〕が進んでいるということだ。
B 複雑化
C 帰化
D 簡略化
言語⑥:長文読解
( i )
( ii )
( iii )
A
道徳的
経済的
普遍的
B
道徳的
普遍的
経済的
C
普遍的
道徳的
経済的
D
普遍的
経済的
道徳的
E
経済的
普遍的
道徳的
A:アだけ
B:イだけ
C:ウだけ
D:アとイ
E:アとウ
F:イとウ
A:アだけ
B:イだけ
C:ウだけ
D:アとイ
E:アとウ
F:イとウ
A:アだけ
B:イだけ
C:ウだけ
D:アとイ
E:アとウ
F:イとウ
言語⑦:熟語の成り立ち
B 動詞の後に目的語をおく
C 似た意味を持つ漢字を重ねる
D 反対の意味を持つ漢字を重ねる
E 前の漢字が後の漢字を修飾する
A:反対の意味を持つ漢字を重ねる
B:主語と述語の関係にある
C:動詞の後に目的語をおく
D:上記のどれにも当てはまらない
A:反対の意味を持つ漢字を重ねる
B:主語と述語の関係にある
C:動詞の後に目的語をおく
D:上記のどれにも当てはまらない
A:反対の意味を持つ漢字を重ねる
B:主語と述語の関係にある
C:動詞の後に目的語をおく
D:上記のどれにも当てはまらない
A:前の漢字が後の漢字を修飾する
B:似た意味の漢字を重ねる
C:動詞の後に目的語をおく
D:上記のどれにも当てはまらない
A:前の漢字が後の漢字を修飾する
B:似た意味の漢字を重ねる
C:反対の意味の漢字を重ねる
D:上記のどれにも当てはまらない
似た意味を持つ漢字を重ねた熟語
安穏
あんのん
隠匿
いんとく
隠蔽
いんぺい
永久
えいきゅう
恩恵
おんけい
温暖
おんだん
絵画
かいが
学習
がくしゅう
隔離
かくり
河川
かせん
岩石
がんせき
願望
がんぼう
陥没
かんぼつ
寒冷
かんれい
奇怪
きかい
犠牲
ぎせい
基礎
きそ
救助
きゅうじょ
脅威
きょうい
競争
きょうそう
計測
けいそく
反対の意味を持つ漢字を重ねた熟語
哀歓
あいかん
異同
いどう
因果
いんが
栄枯
えいこ
遠近
えんきん
往復
おうふく
開閉
かいへい
加減
かげん
緩急
かんきゅう
乾湿
かんしつ
寒暖
かんだん
緩慢
かんまん
吉凶
きっきょう
起伏
きふく
及落
きゅうらく
強弱
きょうじゃく
去就
きょしゅう
屈伸
くっしん
苦楽
くらく
慶弔
けいちょう
好悪
こうお
功罪
こうざい
公私
こうし
攻守
こうしゅ
高低
こうてい
呼応
こおう
左右
さゆう
縦横
じゅうおう
衆寡
しゅうか
需給
じゅきゅう
授受
じゅじゅ
出没
しゅつぼつ
首尾
しゅび
上下
じょうげ
真偽
しんぎ
新旧
しんきゅう
親疎
しんそ
進退
しんたい
出納
すいとう
盛衰
せいすい
精粗
せいそ
善悪
ぜんあく
送迎
そうげい
粗密
そみつ
損得
そんとく
貸借
たいしゃく
大小
だいしょう
諾否
だくひ
男女
だんじょ
難易
なんい
貧富
ひんぷ
夫妻
ふさい
父母
ふぼ
抑揚
よくよう
主語と述語の関係にある熟語
円高
えんだか
円安
えんやす
官営
かんえい
官製
かんせい
県立
けんりつ
国営
こくえい
国立
こくりつ
骨折
こっせつ
市営
しえい
地震
じしん
私立
しりつ
市立
しりつ
神授
しんじゅ
人造
じんぞう
頭痛
ずつう
天授
てんじゅ
都立
とりつ
日没
にちぼつ
日照
にっしょう
年少
ねんしょう
年長
ねんちょう
腹痛
ふくつう
雷鳴
らいめい
動詞の後に目的語をおく
握手
あくしゅ
営業
えいぎょう
越冬
えっとう
閲兵
えっぺい
延期
えんき
懐疑
かいぎ
開会
かいかい
開店
かいてん
開門
かいもん
架橋
かきょう
加熱
かねつ
観劇
かんげき
帰国
きこく
喫茶
きっさ
求人
きゅうじん
仰天
ぎょうてん
享楽
きょうらく
禁煙
きんえん
減刑
げんけい
懸命
けんめい
採光
さいこう
在宅
ざいたく
作文
さくぶん
止血
しけつ
遮光
しゃこう
借金
しゃっきん
就職
しゅうしょく
修業
しゅぎょう
遮光
しゃこう
受賞
じゅしょう
殉難
じゅんなん
譲位
じょうい
消火
しょうか
乗車
じょうしゃ
植樹
しょくじゅ
叙勲
じょくん
叙景
じょけい
除湿
じょしつ
炊飯
すいはん
惜別
せきべつ
洗顔
せんがん
潜水
せんすい
宣誓
せんせい
遭難
そうなん
脱帽
だつぼう
着席
ちゃくせき
挑戦
ちょうせん
徹夜
てつや
点火
てんか
投球
とうきゅう
登校
とうこう
読書
どくしょ
登山
とざん
渡米
とべい
日没
にちぼつ
入魂
にゅうこん
忍苦
にんく
破戒
はかい
避難
ひなん
閉店
へいてん
冒険
ぼうけん
前の漢字が後の漢字を修飾する熟語
悪評
あくひょう
暗示
あんじ
異国
いこく
遠路
えんろ
大空
おおぞら
屋外
おくがい
屋内
おくない
温泉
おんせん
概観
がいかん
海水
かいすい
仮定
かてい
過程
かてい
下流
かりゅう
奇遇
きぐう
机上
きじょう
既成
きせい
急病
きゅうびょう
貴賓
きひん
急逝
きゅうせい
強風
きょうふう
曲線
きょくせん
偶発
ぐうはつ
軽傷
けいしょう
激流
げきりゅう
傑作
けっさく
厳封
げんぷう
高温
こうおん
公害
こうがい
好感
こうかん
高山
こうざん
後退
こうたい
黒板
こくばん
互譲
ごじょう
最悪
さいあく
再会
さいかい
最高
さいこう
室外
しつがい
実施
じっし
室内
しつない
借金
しゃっきん
住人
じゅうにん
俊足
しゅんそく
上空
じょうくう
上流
じょうりゅう
少量
しょうりょう
深海
しんかい
深紅
しんく
辛勝
しんしょう
新年
しんねん
親友
しんゆう
生物
せいぶつ
漸進
ぜんしん
前進
ぜんしん
打球
だきゅう
直線
ちょくせん
直角
ちょっかく
追伸
ついしん
初雪
はつゆき
微笑
びしょう
頻発
ひんぱつ
併記
へいき
猛獣
もうじゅう
洋画
ようが
予知
よち
冷水
れいすい
廉価
れんか
老人
ろうじん
和食
わしょく
言語⑧:二字熟語
2 言質 げんち あとで証拠となる約束の言葉
3 不憫 ふびん かわいそうで哀れむべきこと
4 沿革 えんかく 物事の移り変わり
5 断腸 だんちょう はらわたがちぎれるほど、非常に悲しいこと
6 雄飛 ゆうひ 勇ましく盛んに活動すること
7 罷免 ひめん 職をやめさせること。免職
8 席捲 せっけん はげしい勢いで、自分の勢力範囲をひろげること
9 顧慮 こりょ 考慮に入れて心遣いをすること。気づかうこと
10 邂逅 かいこう 思いがけなく会うこと。めぐりあい
11 釈然 しゃくぜん 疑い・恨みなどが消えて心が晴れ晴れするさま
12 透徹 とうてつ 澄んで濁りのないこと。筋が通っていてはっきりしていること
13 鳥瞰 ちょうかん 高い所から見下ろすこと。また全体を見渡すこと
14 斯界 しかい この社会。その道その道の専門の社会。この道。この方面。
15 逓減 ていげん しだいに減ること。だんだんに減らすこと。
16 老練 ろうれん 多く経験を積んで、物事に慣れ、巧みであること。
17 督励 とくれい 監督し、励ますこと。
18 跳梁 ちょうりょう 跳ね回ること。転じて、好ましくないものがのさばってはびこること。
19 耽読 たんどく 夢中になって読みふけること。
20 暁通 ぎょうつう すみずみまで知り尽くしていること
21 猜疑 さいぎ ねたみ疑うこと。
22 趨勢 すうせい 物事が進んでいく勢い。
23 佳境 かきょう 興味深い場面。おもしろい所。
24 獰悪 どうあく 性質が乱暴で荒っぽいこと。凶悪。
25 励行 れいこう 決めたこと、決められたことをその通りに実行すること。
26 敷延 ふえん 意味や趣旨をおし広げて説明すること。
27 至言 しげん あることがらを非常にうまく、適切に言い表したことば。
28 伝播 でんぱ 広く伝わること
29 漸進 ぜんしん 順を追ってだんだんに進むこと
30 崇高 すうこう 気高く尊いさま
31 脆弱 ぜいじゃく もろくて弱いこと。また、そのさま
32 披瀝 ひれき 心の中の考えをつつみかくさず、打ち明けること。
33 再三 さいさん たびたび、何度も
34 桎梏 しっこく 人々を手かせ足かせのように縛るもの
35 英知 えいち 深遠な道理を知りうるすぐれた知恵
36 垂涎 すいぜん よだれが垂れるほどの欲。ある物を手に入れたいと強く思うこと。
37 僭越 せんえつ 自分の身分や資格を越えて、出過ぎたことをすること。
38 狼狽 ろうばい うろたえ騒ぐこと。あわてふためくこと
39 金言 きんげん 模範となるような優れた格言
40 英断 えいだん 思いきりよく事を決すること。すぐれた決断
41 焦眉 しょうび まゆげを焦がすばかりに火が迫るように、危難が迫ること
42 気鋭 きえい 意気込みが鋭いこと
43 伍する ごする 他者と同等の位置にある。かたをならべる
44 迎合 げいごう 自分の考えを曲げてでも、他人の気に入るように調子を合わせること
45 吹聴 ふいちょう 言いふらすこと
46 殊勝 しゅしょう 心がけや行動などが感心なさま。けなげであるさま
47 粉飾 ふんしょく 立派にみせかけること
48 進言 しんげん 目上の人に対して意見を申し述べること
49 軋轢 あつれき 葛藤の生じること。仲が悪くなること
50 詭弁 きべん 道理に合わないこじつけの弁論
51 会得 えとく 物事の意味、本質などを理解し悟ること
52 符合 ふごう 完全に一致すること
53 流布 るふ 世間に広まること。広く知れ渡ること。
54 躍如 やくじょ 生き生きと現れているさま
55 至言 しげん いかにも正しいところを言いあてた言葉
56 委細 いさい くわしいこと。こまごましたくわしい事情
57 謬見 びゅうけん まちがった考えや見解
58 狡猾 こうかつ 悪賢いこと
59 公算 こうさん 偶然に支配される事柄の、生起の確実性の度合。
60 看破 かんぱ 見やぶること。
61 卑近 ひきん 身近でありふれていること。高尚でなくわかりやすいこと。
62 困憊 こんぱい 苦しいこと続きに疲れ果てること
63 尊大 そんだい 人を見下したような偉そうな態度をとること
64 憐憫 れんびん ふびんに思うこと。あわれみの気持ち
65 営々 えいえい せっせと一生懸命に働くさま
66 胆勇 たんゆう ものに動じない勇気があること
67 比肩 ひけん 肩を並べること。同等なこと
68 出色 しゅっしょく きわだって他よりすぐれていること。
69 泰然 たいぜん 落ち着いていて物事に動じない様子
70 腐心 ふしん 心をなやますこと。ひどく心を使うこと
71 斡旋 あっせん 間に入って両者をうまくとりもつこと
72 雌伏 しふく 力を養い、自分の活躍する機会を待つこと
73 回顧 かいこ 過去を振り返ること
74 安泰 あんたい やすらかで穏やかなこと
75 恭順 きょうじゅん 命令につつしんで従う態度をとること
76 呵責 かしゃく 責め苦しめること。しかり責めること
77 杞憂 きゆう 心配しないでいい事を心配すること。とりこし苦労
78 傀儡 かいらい あやつり人形。くぐつ。でく。
79 甘受 かんじゅ 甘んじて受けること
80 機知 きち その場に応じてとっさに働く鋭い知恵
81 漸次 ぜんじ 次第に。だんだん
82 懐柔 かいじゅう うまく手なずけ従わせること
83 義憤 ぎふん 道にはずれたことに対して発するいかり
84 奸知 かんち ずる賢い知恵
85 進取 しんしゅ 進んでことをなすこと。進んで物事にとりくんで行くこと。
86 闊達 かったつ 度量が大きくて、小さな物事にこだわらないさま。
87 啓蒙 けいもう 人々に正しい知識を与え、教え導くこと
88 新鋭 しんえい 新しく現れ、勢いが強いこと
89 誇示 こじ 自慢して見せること
90 奔流 ほんりゅう 勢いの激しい流れ言語⑨:四字熟語
2 胆大心小 たんだいしんしょう 度胸は大きく、注意は細かくすべきこと
3 孤立無援 こりつむえん 仲間もなく助けてくれるものがいないこと
4 七転八倒 しちてんばっとう 転がりまわって、苦しむこと
5 意気消沈 いきしょうちん 元気をなくし沈み込むこと
6 神出鬼没 しんしゅつきぼつ 行動が自由自在で、所在などが容易に計り知れないこと
7 清廉潔白 せいれんけっぱく 心や行いがきれいで後ろ暗いところのないこと
8 融通無碍 ゆうずうむげ 一定の考え方にとらわれることなく、自由にどんな事態にも対応できること
9 暴虎馮河 ぼうこひょうが 向こう見ずに命知らずのことをすること
10 無知蒙昧 むちもうまい 学問がなく、物事の道理にくらいこと
11 森羅万象 しんらばんしょう 宇宙に存在する数限りない全てのもの
12 虚心坦懐 きょしんたんかい 何のわだかまりもない素直なさっぱりした心で物事に臨むさま
13 明鏡止水 めいきょうしすい 何のわだかまりもない、静かに澄みきった心の状態
14 当意即妙 とういそくみょう その場にうまく適応して機転をきかすこと
15 単刀直入 たんとうちょくにゅう いきなり問題の要点に入ること
16 理路整然 りろせいぜん 話や考えの筋道がきちんと通っているさま
17 七難八苦 しちなんはっく さまざまな苦難。多くの苦難が重なること
18 百花繚乱 ひゃっかりょうらん 優れた人や業績などが一時期にたくさん現れること
19 一挙両得 いっきょりょうとく 1つの事をして同時に2つの利益を得ること
20 内憂外患 ないゆうがいかん 国内にある心配事と国際上の心配事
21 無念無想 むねんむそう 無心。一切の妄念を離れること
22 破顔一笑 はがんいっしょう 顔をほころばせてにっこり笑うこと
23 右往左往 うおうさおう うろたえてあちらへ行ったりこちらへ行ったりすること
24 泰然自若 たいぜんじじゃく 落ち着き払っていて平常と変わらないさま
25 試行錯誤 しこうさくご 種々の方法を試み、失敗を繰り返しながら目的に向かって解決方法を追求すること
26 支離滅裂 しりめつれつ 物事に一貫性がなく、ばらばらに乱れて筋道が立たないさま
27 七転八起 しちてんはっき 何度失敗してもくじけず、たちあがって奮闘すること
28 朝三暮四 ちょうさんぼし 目先の違いに気をとられて、同じ結果となるのに気づかないこと
29 竜頭蛇尾 りゅうとうだび 始めは盛んだが、終わりの振るわないこと
30 徹頭徹尾 てっとうてつび 始めから終わりまで徹底しているさま
31 和洋折衷 わようせっちゅう 日本風と西洋風をほどよく取り合わせること
32 電光石火 でんこうせっか 動作などが非常に迅速なさま
33 自縄自縛 じじょうじばく 自分の言動や心がけによって、自分自身動きがとれなくなること
34 千載一遇 せんざいいちぐう 千年に一度しかめぐりあえないような、めったにない機会
35 荒唐無稽 こうとうむけい 言動や考えに根拠がなく現実味のないこと
36 魑魅魍魎 ちみもうりょう 山の怪物や川の怪物、様々な化け物
37 勢力伯仲 せいりょくはくちゅう 互いの力が接近していて優劣がつけにくいこと
38 絶体絶命 ぜったいぜつめい 追い詰められて逃れられない困難な立場にあること
39 唯唯諾諾 いいだくだく ただただ人の意見に盲従するさま。言いなりになること
40 四面楚歌 しめんそか まわりが敵ばかりで孤立してしまうこと
41 前代未聞 ぜんだいみもん これまでに一度も聞いたことがないこと
42 晴耕雨読 せいこううどく 自適の生活を送ること
43 天衣無縫 てんいむほう 詩や文章などに技巧を凝らしたあとがなく、自然で完美であるさま
44 一言一句 いちごんいっく 一つひとつの言葉のこと
45 本末転倒 ほんまつてんとう 根本的で重要な事柄と些細なつまらない事柄とを取り違えること
46 一心不乱 いっしんふらん 1つのことに心を集中して他に気をとられないこと
47 意気投合 いきとうごう 互いの気持ちがぴったりと合って仲良くなること
48 自業自得 じごうじとく 自分のしたことが原因で自ら受ける苦しみや災難のたとえ
49 天変地異 てんぺんちい 台風や地震など、天地間の自然の異変
50 自画自賛 じがじさん 自分で自分のことをほめること言語⑩:文節の並び替え